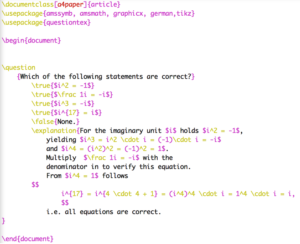
5.1 – Sinn und Zweck

Interaktive Elemente

helfen den Studierenden, formalisierte mathematische Prinzipien und Konzepte in einer dynamischen Form zu erfassen. Sie können Parameter und Funktionen selbstständig manipulieren und so die Veränderungen zum Beispiel visuell wahrnehmen.
Der Inhalt lässt sich als Prozess besser nachvollziehen. Die Formeln werden vom Modus der Symbolsprache in einen dynamischen Modus transformiert.

Damit können auch unterschiedliche Lerntypen unterstützt werden:

Anfänger/innen, welche sich zu Beginn des Studiums noch nicht auf einem hohen Abstraktionsniveau bewegen, erfahren eine schnelle erste Anschauung eines bis dahin unbekannten Objektes. Ohne diese Begleitung ist die/der Einzelne oft nicht in der Lage, Bezüge zwischen der Darstellung und dem mathematischen Inhalt herzustellen.
Auch Studierende, welchen Mathematik leichter fällt, profitieren: Sie können auf dem visuellen Wahrnehmungskanal das bisher Verstandene überprüfen und vertiefen.

Dozierende

verfügen in der Präsenzveranstaltung über interaktive, dynamische Erklärungen statt statischer und oft aufwendiger Tafelbilder.
Sie sind entlastet von Routinearbeiten, und es entsteht freie Zeit für anspruchsvollere Lehre und Betreuung der Studierenden.

Wir stellen hier einige interaktive Elemente und deren Einsatz vor.

5.2 – Interaktive Aufgaben

Solche Aufgaben sind dadurch ckarakterisiert, dass es auf die Eingabe der Studierenden eine automatisierte und möglichst personalisierte Rückmeldung gibt. Die Eingabe erfolgt zum Beispiel einmalig mit einer Bewertung oder in einem Quiz-Modus mit beliebiger Wiederholung.

5.2.1 – Multiple-Choice-Aufgaben

Mehrwert für Studierende

Die MC-Aufgaben

regen die Studierenden an, mathematische Probleme eigenständig zu lösen. Die MC-Antwortvorgaben verlangen aber von ihnen auch eine präzisere Bearbeitung.
geben ein unmittelbares und eindeutiges Feedback auf die Lernleistungen. Studierende können ihren Leistungsstand einschätzen und das weitere Lernen planen. Die Lösungen sollten dabei so differenziert sein, dass die Studierenden erkennen können, wo Entwicklungsbedarf besteht und sie gezielt Unterstützung bei Mitstudierenden oder Lehrenden einholen sollten.
unterstützen durch unmittelbare Rückmeldungen und eine partielle Individualisierung den Lernprozess.

Dieses Angebot zeigt den Studierenden, wie ihre Leistungen im Vergleich zu den Mitstudierenden stehen, was im Hinblick auf die Prüfungen bedeutsam ist.

Mehrwert für Dozierende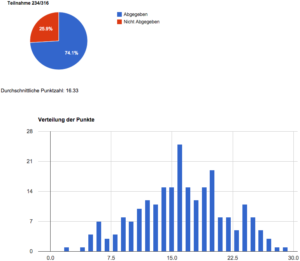

Die Dozierenden

erhalten detaillierte statistische Auswertungen über die Kompetenzen der Studierenden.
ersehen, bei welchen Aufgaben typische und/oder systematische Probleme auftreten und
können anhand dieser Kenntnisse die Lehrveranstaltung adaptiv planen, modifizieren und bei Bedarf verbessern. Unklarheiten, fehlende Denkschritte usw. können aufgegriffen und geklärt werden.

5.2.2 – Erstellung und Veröffentlichung

Echo

Um die eingeschränkte Darstellung der Mathematik in Moodle und das barrierefreie Arbeiten mit LaTeX zu ermöglichen, steht am D-MATH die Echo-Umgebung zur Verfügung.

Clicker / Edu-App

Die Clicker-Funktion der Edu-App erlaubt, niederschwellig MC-Fragen in der Präsenzveranstaltung zu stellen. Die Ergebnisse regen dann zur Diskussion mit den Studierenden an.

Moodle

Die Lernplattform Moodle an der ETH bietet MC-Aufgaben an. Am D-MATH haben wir ein spezielles Moodle-Plugin entwickelt.

5.2.3 – Interaktive (Khan-)Aufgaben

Aufgaben mit einem höheren Interaktionsgrad als MC ermöglichen den Studierenden, personalisierte Aufgaben mit direkter Rückmeldung (wiederholt) zu trainieren, mit integrierter Validierung der Ergebnisse und jeweils neu generierten Zahlenwerten.

Im Moment konzentrieren wir uns auf die Angebote der Khan-Acadamy.

Hier stehen die Eingaben von Zahlen oder symbolischen Ausdrücken zur Verfügung – auch MC mit dynamischen Werten sowie graphischen Komponenten.

Die Darstellung der Lösung erfolgt schrittweise durch die eigenständige Kontrolle der Anwender.

Die Dozierenden und Assistierenden werden durch den Einsatz von individualisierenden Routinekorrekturen entlastet und erhalten somit mehr Zeit für anspruchsvollere Betreuungs- und Lehrtätigkeiten. Sie können zum Beispiel in der Vorlesung anhand ausgewählter Zahlen Besonderheiten vorstellen und diskutieren.

Einsatz

Eine Anwendung findet sich im Rahmen des Brückenkurses.

Die Aufgaben sind nicht auf Schulmathematik begrenzt: Die Erstellung solcher Khan-Aufgaben basiert auf Java-Skript. Eine Vorlage für den eigenen weiterführenden Einsatz kann bei Alexander Caspar oder Heinz Rasched via echo@ethz.ch bezogen werden.

Zur Zeit sind solche Aufgaben für das Basis-Jahr in Vorbereitung.

Alternativen

Als Variante der hier besprochenen Khan-Aufgaben gibt es gerade für anspruchsvollere Aufgaben die Möglichkeit, Lösungen so aufzubereiten, dass die Studierenden Schritt für Schritt durch eine Aufgabe geführt werden, bei jedem Schritt aber selbst entscheiden können, ob sie zusätzliche Hilfe und Hinweise brachen oder nicht. Diese zusätzliche Hilfe kann z. B. durch eingebundene Audio-Files oder durch Pop-ups realisiert werden. Die Idee dabei ist, dass diese Hilfe nicht einfach so schon dasteht, die Eigenverantwortung, selbst über die Problematik nachzudenken, soll also gefördert werden.

Ein Beispiel eines solchen Ansatzes findet sich im untenstehenden Dokument (bitte mit AcrobatReader öffnen).

Weitere Beispiele, Varianten und eine weiterführende Diskussion dieser Thematik findet der/die interessierte Leser/in in Laura Kellers Blog

5.3 – Kleine Applets

Eine weitere interaktive Lehrmöglichkeit bieten kleine Applets, bei denen «mathematische Effekte»an ausgewählten Beispielen direkt erlebt werden können.

Im Beispiel kann der Einfluss der Parameter auf die (graphischen) Eigenschaften von drei exemplarischen Funktionen direkt beobachtet werden (mit den Reglern können die Parameter verstellt werden).

Das oben verlinkte Beispiel wurde mit dem Programm GeoGebra erstellt.

Mehr zu diesen Applets findet der/die interessierte Leser/in im nächsten Kapitel.

5.4 – Interaktive Lerninhalte mit H5P

Im ETH eSkript sowie in der Lernplattform Moodle können Interaktive H5P Inhalte eingebunden werden. Ein Beispiel dafür sind sogenannten interaktive Präsentationen, wo einer Präsentation gezielt Fragen hinzugefügt werden können. Diese erlauben es dem Dozierenden, in regelmässigen Abständen die Studierenden zu den Kernpunkten abzufragen. Weiter erhält der Student ein direktes Feedback, ob er die Kernpunkte des Stoffes verstanden hat. Für die Form der Fragen gibt es verschiedene Möglichkeiten wie z.B. Multiple-Choice und Lückentests.

Hier eine kurze Illustration einer interaktiven Präsentationen:

Mehr Beispiele findet man auf dem ETH eSkript Howto (Interactivity Modules).

Eine knappe Anleitung zur Erstellung einer interaktiven Präsentation findet man hier. Bei weiteren Fragen steht Roger Käppeli gerne zur Verfügung.
Es gibt etliche weitere Möglichkeiten, und wir verweisen auf https://h5p.org für mehr Informationen.

5.5 – Programmieraufgaben

Ähnlich wie traditionelle Papier-und-Bleistift-Aufgaben (P&BA) sollen auch Programmieraufgaben (PA) den Studenten ermöglichen, das in der Vorlesung gesammelte passive Wissen in aktives Wissen zu verwandeln. Jedoch weisen letztere Aufgaben ein paar zusätzliche Ansprüche auf:

Hardware- und Software-Voraussetzungen
Um PA zu bearbeiten, ist es für den Studierenden zwingend, Zugang zu einem Personal Computer mit der benötigten Software zu haben.
Die Software-Installation auf dem eigenen Rechner, zusammen mit der eventuellen Lizenzbeschaffung, kann sich als zeitintensiv erweisen. Für den Studierenden machen diese Voraussetzungen die Einstiegsschwelle um einiges höher bei PA als bei traditionellen P&BA. Alternativ stehen die Rechner in den Computer-Räumen (mit aller benötigter Software) zur Verfügung. Der Zugang zu diesen ist jedoch an die Gebäudeöffnungszeiten gebunden.
Publikation, Abgabe, Korrektur und Rückgabe
Für den Dozierenden kann die Publikation der PA auf dieselbe Art und Weise geschehen wie bei P&BA, ausser dass man für ersteres eventuelle Vorlagen (Templates) zur Verfügung stellen möchte. Für die Studierenden ändert sich gegenüber P&BA nichts (oder wenig wie z.B. ein Download der Vorlagen/Templates). Obwohl Abgabe, Korrektur und Rückgabe der PA prinzipiell in Papierform möglich ist, d.h. wie bei bzw. mit den P&BA im Übungsfächlein, ist diese Form jedoch eher schlecht geeignet. Z.B. würde die Korrektur nur auf sehr oberflächlichem Niveau geschehen (das Programm sieht auf Papier aus, als ob es ungefähr funktionieren könnte), oder Korrigierende müssen auf mühsame Art und Weise Programmabschnitte eintippen und testen.

Auf einige der oben erwähnten Punkte gehen wir im Folgenden ein und skizzieren mögliche Ansätze.

Für Fragen steht Roger Käppeli gerne zur Verfügung.

5.5.1 – Hardware- und Software-Voraussetzungen

Heutzutage besitzen die meisten (alle) Studierenden einen Personal Computer in der Form eines Laptops. Diese können zu erschwinglichen Preisen z.B. beim Projekt Neptun erworben werden.

Die benötigte Software für die PA hängt von der verwendeten Programmiersprache ab. Im Folgenden ein paar illustrative Beispiele.

Häufig wird bei Einführungsvorlesungen (Lineare Algebra, Numerik, …) die kommerzielle Software MATLAB verwendet. Diese erfordert eine gültige Lizenz, welche die Studierenden im IT Shop der ETH beziehen können. MATLAB kann auf allen gängigen Betriebssystemen (Windows/OSX/Linux) relativ problemlos installiert werden. Die Nutzung wird meistens in der ersten Übungsstunde in der Form eines kurzen Tutorials eingeführt.

Für Studierende/Dozierende, welche auf den Einsatz kommerzieller Software lieber verzichten, gibt es den freien MATLAB-Klon GNU Octave, dessen Programmiersyntax weitgehend zu dem proprietären MATLAB kompatibel ist.

PYTHON ist eine interpretierte höhere Programmiersprache, welche mit den SciPy Paketen NumPy und matplotlib bestens zur Lehre vom wissenschaftlichen Rechnen geeignet ist. PYTHON und SciPy sind Open Source und damit frei erhältlich.

Zur Installation gibt es mehrere Möglichkeiten: Zwei All-in-one Lösungen für alle gängigen Betriebssysteme (Windows/OSX/Linux) sind geboten durch Enthought Canopy und Anaconda. Diese sind frei zugänglich, bieten aber kommerziellen Support an.

Für Vorlesungen, wo eine kompilierte Programmiersprache (C, C++, …) eingesetzt wird, kann die anfängliche Softwareinstallation wesentlich komplizierter werden. Eine mögliche Lösung bieten hier sog. web-based IDEs wie Codeboard. Letzteres wird an der ETH bereits erfolgreich von einigen Informatik-Dozenten eingesetzt.

5.5.2 – Publikation, Abgabe, Korrektur und Rückgabe

Im Folgenden diskutieren wir mögliche Ansätze zur Publikation, Abgabe, Korrektur und Rückgabe von PA.

Klassische Lösungen

In diesem Fall werden die PA genau wie die P&BA über eine Kurs-Homepage publiziert. Diese sehr einfache Lösung ist universell anwendbar, da sie unabhängig von der verwendeten Software bzw. Programmiersprache ist.
Die Abgabe kann in Papierform (ausgedruckter Quellcode) zusammen mit den P&BA erfolgen (Übungs-Stunde oder -Fächlein). Ein Nachteil ist jedoch, dass die Assistierenden den abgegebenen Quellcode nicht direkt testen können (ein mühsames Abtippen wäre nötig). Korrekturen werden wie bei P&BA auf Papier angebracht und die Rückgabe erfolgt mit den P&BA in der Übungs-Stunde oder im -Fächlein.
Eine Alternative wäre die Abgabe per Email an den zuständigen Assistierenden. Damit erhalten die Assistierenden vollen Zugang zum Quellcode und können ihn gründlich testen. Korrekturen können im Quellcode erfolgen und bieten somit einen wesentlichen Mehrwert. Die Rückgabe erfolgt wiederum per Email. Dies ist jedoch bei grösseren Vorlesungen nur bedingt zu empfehlen weil die Email Flut für die Assistierenden doch schnell unübersichtlich werden kann.

Eine bessere Möglichkeit der Abgabe geht über ein am SAM entwickeltes Webformular: das SAM-UPLOAD-TOOL. Hier auch erhalten die Assistierenden vollen Zugang zum Quellcode, können ihn gründlich testen und Korrekturen können direkt im Quellcode erfolgen. Die Rückgabe erfolgt das SAM-UPLOAD-TOOL.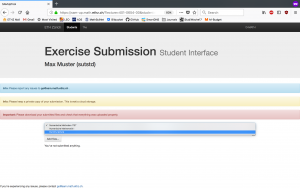

Die Einrichtung des Tools kann sehr einfach auf jede Vorlesung angepasst werden. Falls Sie interessiert sind, kontaktieren Sie Roger Käppeli.

Prinzipiell ist dieses Tool nicht nur für Programmier-Aufgaben geeignet, sonder auch für klassische P&BA. Der Student würde dann entweder ein Scan seiner Aufgaben abgeben, oder, falls er über ein Tablett verfügt, direkt ein auf dem Tablett erstelltes PDF. Viele Assistierende verfügen über ein Tablett worauf die Abgaben der Studierenden direkt korrigiert werden können. Dies würde u.a. den Papierverbrauch senken.

Moodle basierte Lösungen

Hier wird die Lernplattform Moodle verwendet zur Publikation, Abgabe und Rückgabe der PA. Diese Lösung passt prinzipiell gut zu beiden Typen von Aufgaben (P&BA und PA) und ist unabhängig von der verwendeten Software bzw. Programmiersprache.

In einem Moodle Kurs kann man Aufgaben/Serien (zusammen mit Templates) elektronisch publizieren. Weiter können auch Abgabefristen definiert werden.

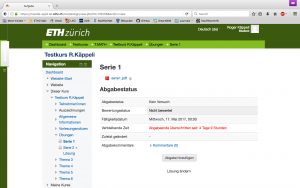Die Assistierenden erhalten die Rolle eines «Non-editing Teacher», welche es ihnen erlaubt, die abgegebenen Aufgaben einzusehen. Sie haben so vollen Zugang zu dem abgegebenen Quellcode und können diesen ausführlich testen und korrigieren. Die Rückgabe der korrigierten Aufgaben/Serien kann auch direkt wieder über die Moodle Plattform erfolgen.

git basierte Lösungen

Bei dieser Variante wird die Versionsverwaltung Software git verwendet zur Publikation, Abgabe und Rückgabe der PA. Als Managementsystem wird dafür der D-MATH GitLab Service verwendet. Diese Lösung ist unabhängig von der verwendeten Software bzw. Programmiersprache anwendbar .

Einen kurzen Einblick in den Arbeitsablauf dieser Lösung findet man z.B. auf https://classroom.github.com.

Wegen der zusätzlichen Schwierigkeit der Bedienung einer Versionsverwaltungs-Software ist diese Lösung jedoch eher für Studienrichtungen mit einem besonderen Schwerpunkt auf Computer Simulationen und Software Entwicklung wie z.B. für die RW/CSE Studierenden geeignet. Der Mehrwert dieser Lösung besteht darin, dass die Studierenden in einer berufs- und praxis-nahen Umgebung lernen zu arbeiten.

5.5.3 – Interaktion unter Studierenden / mit Assistierenden

Eine interessante Applikation zur Verbesserung und Unterstützung der Interaktion, insbesondere der virtuellen Interaktion, zwischen Studierenden oder mit Assistierenden bietet die an der ETH entwickelte Applikation TeachRemote (siehe https://www.teachremote.ch , oder diese PDF-Dokumentation zu TeachRemote).

Wer keine zusätzliche Applikation installieren möchte und auf die weit an der ETH verbreitete Video-Kommunikationsplattform Zoom zurückgreifen möchte, kann dies selbstverständlich tun. Ein paar praktische Tipps, wie es gut gelingt, gegenseitig (von Hand) geschriebene Notizen via Zoom zu teilen, findet man entweder unter Video praktischer Tipp 1 oder unter Video praktischer Tipp 2 .

5 Interaktivitäten – Diskussion und Illustrationen