Bisher haben wir gesehen, dass wir komplexe Zahlen schreiben können als [latex]z=a+bi[/latex] (mit [latex]a,b, \in \mathbb{R}[/latex]; Real- und Imaginärteil). Diese Darstellung nennt man auch Normalform oder kartesische Form.
Ausserdem haben wir gesehen, dass komplexe Zahlen in der komplexe Ebene – auch Gaussschen Ebene genannt, geometrisch veranschaulicht werden können. Wir haben dabei den Realteil auf der [latex]x[/latex]-Achse und den Imaginärteil auf der [latex]y[/latex]-Achse abgetragen.
Im Folgenden erörtern wir die Frage, ob und wie komplexe Zahlen auch anders dargestellt, respektive beschrieben werden könne. Dies wird uns aufs Stichwort der Polarkoordinaten führen.
Die Idee der Polarkoordinaten ist sehr wichtig, nicht nur für komplexe Zahlen sondern fast immer, wenn man sich mit der Ebene beschäftigt. Diese Darstellung hilft insbesondere, die Multiplikation und das Wurzelziehen besser zu verstehen.
Die grundsätzliche Idee ist sehr einfach. Jeder Punkt in der Ebene lässt sich beschreiben durch
- seinen Abstand zum Ursprung, das heisst, den Betrag
- und einen Winkel (seine «Richtung»). Dieser Winkel ist gerade der Winkel, welcher von der positiven reellen Achse und dem Strahl durch den Ursprung und den betrachteten Punkt eingeschlossen wird. Dieser Winkel wird auch Polarwinkel genannt.
Sei [latex]z=a+bi[/latex]. Die untenstehende Abbildung illustriert die obige Beschreibung.
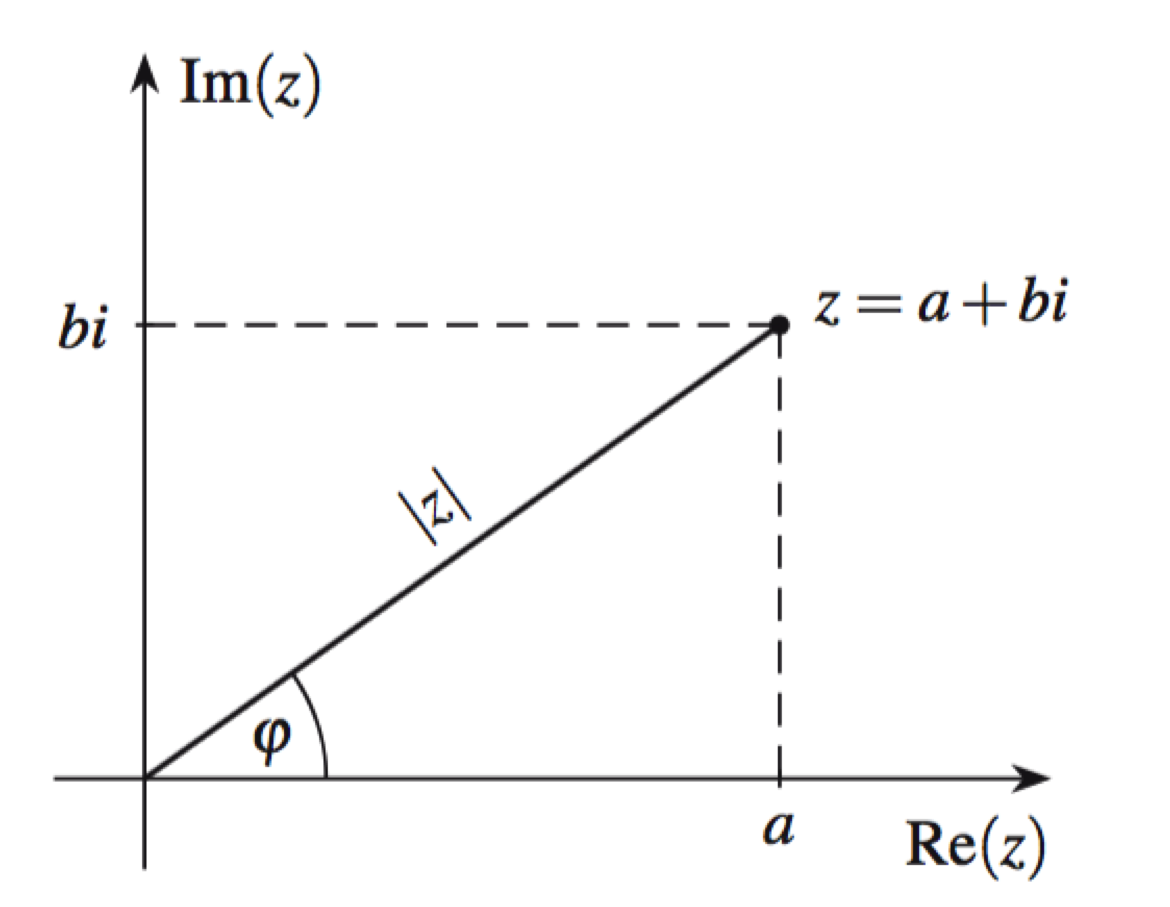
Den Betrag [latex]\left |{z}\right |=r=\sqrt {a^{2}+b^{2}}[/latex] haben wir schon erklärt. Ausserdem haben wir einen Winkel [latex]\varphi[/latex] zwischen dem entsprechenden Vektor [latex]z[/latex] und der positiven reellen Achse.
Bemerkung
Der Winkel [latex]\varphi[/latex] ist nur bis auf ein Vielfaches von [latex]2\pi[/latex] bestimmt. Zum Beispiel liefert für [latex]z = 1+i[/latex] jeder der folgenden Winkel eine korrekte Beschreibung des entsprechenden Punktes:
Oder es gilt für [latex]z =i[/latex]
[latex]\begin{aligned}[]\varphi=\frac {\pi }{2}\text { oder }\frac {\pi }{2}- 2\pi \text { oder }\frac {\pi }{2}+2\pi \text { oder }\frac {\pi }{2}+2\pi k\text { für }k\in \mathbb {Z}.\end{aligned}[/latex]
Wenn Sie noch Mühe haben mit dem Begriff Bogenmass oder mit dem Umrechnen vom Grad nach Bogenmass, dann schauen Sie nach im Brückenkurs im Skript oder bei den dazu passenden Aufgaben.Wenn wir fordern, dass der Winkel in einem Intervall der Länge [latex]2\pi[/latex] liegt, wird er eindeutig. Wir legen hier fest:
Definition
Der Winkel [latex]\varphi[/latex] mit [latex]-\pi \lt \varphi \leq \pi[/latex] heisst das Argument von [latex]z[/latex]:
[latex]\begin{aligned}[]\varphi=\arg(z) \in (-\pi,\pi]\end{aligned}.[/latex]
Achtung: Dies ist eine Wahl des Argumentintervalls. Eine andere populäre Wahl ist
[latex]\varphi=\arg(z) \in [0,2\pi).[/latex]
Auf dem Bild oben sehen wir, dass
gilt. Und somit
[latex]\begin{aligned}[]\varphi =\arctan\left (\frac {b}{a}\right )\label{eq:arctan-1}\end{aligned}[/latex]
wobei [latex]arctan[/latex] die Umkehrfunktion der Tangensfunktion ist. Beachten Sie, dass [latex]\arctan[/latex] Werte im Intervall [latex]\left (-\frac {\pi }{2},\frac {\pi }{2}\right )[/latex] annimmt. Deshalb stimmt (4.1) nur, wenn [latex]\arg(z)\in \left (\frac {-\pi }{2},\frac {\pi }{2}\right )[/latex]. Das gilt genau dann, wenn [latex]z=a+bi[/latex] in der rechten Halbebene liegt, also wenn [latex]a>0[/latex]. Das heisst, die komplexe Zahl liegt im I. oder IV. Quadranten.
Wenn [latex]z=a+bi[/latex] in der linken Halbebene liegt, also wenn [latex]a\lt 0,[/latex] müssen wir die Fälle [latex]b > 0[/latex] und [latex]b\lt 0[/latex] unterscheiden, das heisst, ob die Zahl im II. oder III. Quadranten liegt:
- Im II. Quadranten müssen wir den Winkel um [latex]\pi[/latex] ([latex]180^\circ[/latex] Grad) verschieben, das heisst, wir haben[latex]\begin{aligned}[]\varphi =\arg(a+bi)=\arctan \frac {b}{a}+\pi .\end{aligned}[/latex]
- Im III. Quadranten müssen wir den Winkel um [latex]-\pi[/latex] verschieben, das heisst, wir haben[latex]\begin{aligned}[]\varphi =\arg(a+bi)=\arctan \frac {b}{a}-\pi .\end{aligned}[/latex]
Ist [latex]a=0[/latex], dann liegt die Zahl auf der vertikalen Achse und hat die Form [latex]bi[/latex]. Dann gilt
Das Argument von [latex]0=0+0i[/latex] ist nicht definiert.
Damit haben wir ein Rezept für das Argument jeder komplexen Zahl. Diese Sache mit dem Argument ist am Anfang nicht ganz einfach. Wir werden uns weiter unten ein paar Beispiele dazu ansehen. Zuerst geben wir einige weitere Definitionen.
Definition
Sei [latex]z[/latex] eine komplexe Zahl. Der Real- und Imaginärteil von [latex]z[/latex] heissen die kartesische Koordinaten von [latex]z[/latex]. Wenn wir sie als [latex]a[/latex] und [latex]b[/latex] bezeichnen, heisst die Darstellung
die algebraische/kartesische Darstellung oder die Normalform von [latex]z[/latex].
Der Betrag [latex]r[/latex] und der Winkel [latex]\varphi[/latex] von [latex]z[/latex] heissen die Polarkoordinaten von [latex]z[/latex].
heisst die Polardarstellung.
Die obigen Überlegungen zum Argument haben uns also gezeigt, wie wir von der Normalform in die Polarform umrechnen können. Dies ist zudem im folgenden Video nochmals zusammengefasst.
Die umgekehrte Umrechnung, nämlich von der Polarform in die Normalform ist dagegen viel einfacher. Offensichtlich gilt
[latex]\begin{aligned}[]a=r\cos \varphi \quad b=r\sin \varphi .\label{eq:von Polar to Normal-1}\end{aligned}[/latex]
Sind die Polarkoordinaten [latex]r[/latex] und [latex]\varphi[/latex] einer komplexen Zahl [latex]z[/latex] gegeben, findet man die Normalform [latex]z=a+ib[/latex] einfach durch (4.2). Dies wird im folgenden Video rekapituliert.
4.1 – Die Eulersche Formel
Bemerkung
Es gibt eine nützliche «Abkürzung». Wir schreiben
[latex]\begin{aligned}[]e^{i\varphi }=\cos \varphi +i\sin \varphi .\label{eq:Cis Gleichheit-1}\end{aligned}[/latex]
Diese Identität nennt man auch die Eulersche Formel.
Denken Sie zum jetzigen Zeitpunkt an diese Gleichheit wie an eine Definition. Das heisst, denken Sie, dass wir das Folgende geschrieben haben:
das heisst, dass wir die linke Seite durch die rechte Seite definieren. Wenn wir Potenzreihen besprechen, werden wir eine unabhängige Definition der linken Seite geben, und dann zeigen, dass die Gleichheit (4.3) gilt. Mit dieser Abkürzung sieht die Polardarstellung folgendermassen aus:
Wer jetzt schon mehr darüber erfahren möchte, warum die Eulersche Formel gilt, findet im folgenden Video mehr dazu.
Bemerken Sie, dass für jedes [latex]\varphi[/latex] gilt
Deshalb können wir uns in [latex]e^{i\varphi }[/latex] das [latex]\varphi[/latex] als die «Richtung» und [latex]r[/latex] als den «Betrag/Länge» der Zahl/des entsprechenden Vektors vorstellen.
(Un-)Eindeutigkeit der Polarform
Mit Blick auf die Wahl des Argumentes halten wir fest:
Aus der Gleichung [latex]r_1e^{i\varphi_1}=r_2e^{i\varphi_2}[/latex] mit [latex]r_1,r_2>0[/latex] und [latex]\varphi_1,\varphi_2\in\mathbb R[/latex] folgt, dass
- [latex]r_1=r_2[/latex] und
- [latex]\varphi_1=\varphi_2 +2\pi k[/latex] für ein [latex]k\in \mathbb Z[/latex].
Wichtiges Lernziel: Sie sollten beherrschen, wie man die eine Darstellung in die andere umwandelt.
4.2 – Beispiele
Beispiel
In diesem Beispiel wandeln wir eine komplexe Zahlen in der Normalform in die Polardarstellung um. Wir fangen mit [latex]z_{1}=1+i[/latex] an. Da [latex]{\rm Re}(1+i)=1[/latex] und [latex]{\rm Im}(1+i)=1[/latex], entspricht dies dem Punkt [latex](1,1)[/latex] der Zahl [latex]1+i[/latex].
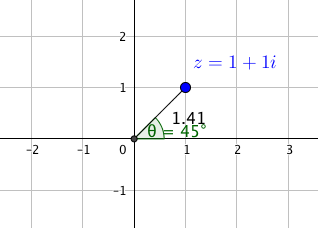
und den Winkel können wir aus dem Bild einfach ablesen
Deshalb ist die Polardarstellung von [latex]z_{1}=1+i[/latex]
Beispiel
Gesucht ist die Polardarstellung von [latex]z_{2}=-3i[/latex].
Lösung:
Da [latex]{\rm Re}(-3i)=0[/latex], liegt der entsprechende Punkt auf der [latex]y[/latex]-Achse. Da [latex]{\rm Im}(-3i)=-3[/latex], entspricht der Punkt [latex](0,-3)[/latex] der Zahl [latex]-3i[/latex]. Hier können beide Polarkoordinaten einfach aus dem Bild abgelesen werden:
Die gesuchte Polardarstellung lautet also:
Beispiel
Was ist die Polarform von [latex]z_{3}=-1+\sqrt {3}i[/latex]?
Lösung:
Man berechnet direkt
und, um den richtigen Wert von [latex]\varphi[/latex] zu finden, muss man überlegen, in welcher Halbebene sich die komplexe Zahl befindet.
Da [latex]{\rm Re}(-1+\sqrt {3}i)=-1\lt 0[/latex], befindet sich die Zahl [latex]z_{3}=-1+\sqrt {3}i[/latex] in der linken Halbebene. Laut dem obigen Rezept gilt
So lautet die Polardarstellung
Die Tatsache, dass [latex]z_{3}=-1+\sqrt {3}i[/latex] in der linken Halbebene liegt, und folglich ihr Winkel zwischen [latex](\frac {\pi }{2},\frac {3\pi }{2})[/latex] liegt, kann man natürlich aus einem Bild sehen:
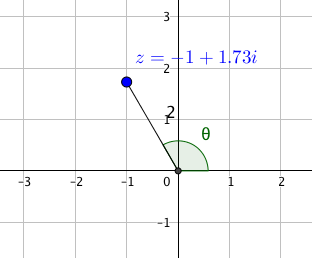
Aber manchmal geht es einfacher mit einer direkten Berechnung.
Beispiel
In diesem Beispiel gehen wir von einer Polardarstellung zu einer algebraischen Darstellung. Die Umformung in diese Richtung ist viel einfacher. Schreiben Sie [latex]{\displaystyle z_{4}=2e^{-\frac {\pi i}{6}}}[/latex] in die Normalform um.
Lösung:
Man muss den Winkel [latex]-\frac {\pi }{6}[/latex] und den Betrag [latex]2[/latex] einfach in (4.2) einsetzen. Einfacher gesagt, benutzt man die Definition von [latex]e^{i\theta }[/latex] und berechnet die Kosinus- und Sinuswerte, um die Zahl in die Form [latex]a+bi[/latex] zu bringen:
Bemerkung
Nach diesen Beispielen lohnt es sich, auf Bemerkung 4.1 zurückzugehen. Dort wird gesagt, dass der Polarwinkel nur bis auf ein Vielfaches von [latex]2\pi[/latex] bestimmt ist. Das können wir aus der Polardarstellung in diesen Beispielen sehen: Für jedes [latex]k\in \mathbb {Z}[/latex] gilt
Also bleibt die Zahl trotz einer Änderung des Winkels um ein Vielfaches von [latex]2\pi[/latex] gleich.
Übungen zu Polarkoordinaten
4.3 – Multiplikation in der Polardarstellung
Mittels Normalform können wir die Addition komplexer Zahlen als Addition von Vektoren veranschaulichen. Hingegen ist es nicht klar, was die geometrische Bedeutung der Multiplikation in Normalform ist. Mittels der Polardarstellung können wir die geometrische Bedeutung leicht verstehen, und dann folgen auch viele wichtige Konsequenzen daraus. Seien [latex]z_{1}[/latex] und [latex]z_{2}[/latex] zwei beliebige komplexe Zahlen und stellen wir sie in Polarkoordinaten dar:
Dann gilt
wobei die Additionstheoreme für Kosinus und Sinus angewandt wurden. Das bedeutet die folgende wichtige Tatsache:
[latex]\begin{aligned}[]r_{1}(\cos \phi _{1}+i\sin \phi _{1})\cdot r_{2}(\cos \phi _{2}+i\sin \phi _{2})=r_{1}r_{2}(\cos (\phi _{1}+\phi _{2})+i\sin (\phi _{1}+\phi _{2}))\label{eq:Multi Formel-1}\end{aligned}[/latex]
Anders gesagt: Das Produkt zweier Zahlen ist gegeben durch die komplexe Zahl, die als Betrag das Produkt der Beträge der Faktoren hat und als Argument die Summe der beiden Winkel.
Mit der Eulerschen Formel ist das letzte Fazit leicht zu verstehen.
[latex]\begin{aligned}[]\underbrace {r_{1}e^{i\phi _{1}}}_{z_{1}}\underbrace {r_{2}e^{i\phi _{2}}}_{z_{2}}=\underbrace {r_{1}r_{2}e^{i(\phi _{1}+\phi _{2})}}_{z_{1}z_{2}}\label{eq:PolarMulti-1}\end{aligned}[/latex]
Spielen Sie mit [latex]z_{1}[/latex] und [latex]z_{2}[/latex] in diesem Applet, um das obige Fazit nachvollziehen zu können.
Übungen zu Polarkoordinaten
4.4 – Potenzen
Sei [latex]z=re^{i\theta }[/latex]. Durch wiederholte Anwendung der Formel (4.4) können wir Potenzen leicht berechnen.
Die einfache Verallgemeinerung hat den folgenden Namen.
Proposition : De Moivre’sche Formel
Ist [latex]z=r(\cos (\theta )+i\sin \theta )[/latex] eine komplexe Zahl und [latex]n\in \mathbb {N}[/latex], so berechnet sich die [latex]n[/latex]-te Potenz von [latex]z[/latex] als
Hier gibt es noch ein passendes Applet, welches die Formel graphisch veranschaulicht:
Beispiel
Berechnen Sie [latex](1+i)^{14}[/latex].
Hinweis: Rechnen Sie lieber ohne die binomische Formel. 🙂
Lösung:
Wir berechnen die Polardarstellung von [latex]1+i[/latex], und dann ist es ein Kinderspiel. Die Polardarstellung haben wir schon gefunden:
Erinnern Sie sich, dass man keinen Arkustangens usw. braucht, um diese Polardarstellung zu finden, sondern nur diese Zahl in der komplexen Ebene einzeichnet, um daraus das Argument und den Betrag ablesen zu können.
Daher haben wir
Was ist in [latex]*[/latex] passiert? Erinnern Sie sich: «Der Polarwinkel ist nur bis auf ein Vielfaches von [latex]2\pi[/latex] bestimmt». Deshalb sollten wir, um den Winkel besser «zu sehen», diesen mit einem Vielfachen von [latex]2\pi[/latex] so verändern, bis er in [latex](-\pi,\pi ][/latex] liegt. So bemerken wir, dass gilt
Dies erklärt nun sofort [latex]*[/latex] .
4.5 – Division
Mit der Polardarstellung können wir auch leicht die Division verstehen. Sei [latex]z=re^{i\theta }[/latex] eine komplexe Zahl, die schon in Polarform gegeben ist.
Was ist die Polardarstellung von [latex]{\displaystyle \frac {1}{z}}[/latex]?
Das heisst, für welche [latex]R[/latex] und [latex]\phi[/latex] gilt [latex]{\displaystyle \frac {1}{z}=R e^{i\phi }}[/latex]?
Offensichtlich lassen sich [latex]R[/latex] und [latex]\phi[/latex] aus der Gleichung [latex]{\displaystyle 1=z\cdot \frac {1}{z}}[/latex] bestimmen. Dazu brauchen wir einfach die Polardarstellung von [latex]1=1+0i[/latex]:
Daraus folgt also [latex]0=\phi +\theta[/latex] und [latex]1=r \cdot R[/latex], so dass [latex]\phi =-\theta[/latex] und [latex]{\displaystyle R =\frac {1}{r}}[/latex].
Fazit: Wenn [latex]{\displaystyle z=re^{i\theta }}[/latex] ist, dann ist [latex]{\displaystyle \frac {1}{z}=\frac {1}{re^{i\theta }}=\frac {1}{r}e^{-i\theta }}[/latex].
Allgemeiner seien [latex]{\displaystyle z_{1}=r_{1}e^{i\phi _{1}}}[/latex] und [latex]{\displaystyle z_{2}=r_{2}e^{i\phi _{2}}}[/latex]. Wir möchten die Polardarstellung von [latex]{\displaystyle \frac {z_{1}}{z_{2}}}[/latex] finden. Dazu merken wir einfach, dass [latex]{\displaystyle \frac {z_{1}}{z_{2}}=z_{1}\cdot \frac {1}{z_{2}}}[/latex] und deshalb
4.6 – Multiplikation mit [latex]e^{i\phi }[/latex]
Es ist nützlich, den Spezialfall der Multiplikation mit [latex]e^{i\phi }[/latex] gut zu verstehen. Zuerst überlegen wir uns, was die Zahl [latex]e^{i\phi }[/latex] ist. Ihr Betrag ist immer [latex]1[/latex], und ihr Polarwinkel ist [latex]\phi[/latex]. Wir möchten wissen, was die geometrische Bedeutung der Multiplikation mit [latex]e^{i\phi }[/latex] ist. Sei [latex]z_{0}=re^{i\theta }[/latex] irgendeine komplexe Zahl. Dann ist
Daher ist die Multiplikation mit [latex]e^{i\phi }[/latex] eine Rotation um den Winkel [latex]\phi[/latex]. Der Betrag ändert sich nicht, und der Winkel wird um [latex]\phi[/latex] grösser bzw. kleiner.
4.7 – Repetition: Rechnen in Polarform
Das folgende Video fasst die gesehenen Rechenregeln nochmals zusammen, die es zu beachten gilt, wenn wir in der Polarform rechnen.
4.8 – Trigonometrische Identitäten
Stellen Sie sich vor, Sie sind gerade bei der Basisprüfung, und Sie brauchen unbedingt die trigonometrische Formel für die Summe zweier Winkel [latex]\alpha[/latex] und [latex]\beta[/latex], und Sie finden diese Identitäten in ihrem Formelbuch nicht. Kein Stress! Wenn Sie sich an die Potenzregeln und an die Eulersche Formel
[latex]\begin{aligned}[]e^{i\theta }=\cos \theta +i\sin \theta \label{eq:euler diff}\end{aligned}[/latex]
erinnern, dann werden Sie leicht zurechtkommen! Hier ist der Trick: Gemäss den Potenzregeln, die selbstverständlich auch im Komplexen gelten, haben wir
Mithilfe von 4.6 bekommen wir
Wir multiplizieren die Klammern aus und klammern [latex]i[/latex] aus
und dann können wir aus dem Realteil (bzw. dem Imaginärteil) die bekannten Formeln ablesen:
Wenn Sie beispielsweise eine Formel für [latex]\sin (n\theta )[/latex] als eine Funktion von [latex]\sin \theta[/latex] und [latex]\cos \theta[/latex] finden möchten, können Sie einfach die Gleichung
benutzen.
Weitere interaktive Übungen
4.9 – Wurzeln
Herleitung eines Rezeptes
Sei [latex]z_{0}=a+ib[/latex] eine komplexe Zahl. Wir suchen nach der [latex]n[/latex]-ten Wurzel von [latex]z_{0}[/latex]. Eine [latex]n[/latex]-te Wurzel von [latex]z_{0}[/latex] ist eine komplexe Zahl [latex]w[/latex] mit
Daher ist die Suche nach der [latex]n[/latex]-ten Wurzel das Gleiche wie die Suche nach den Nullstellen des Polynoms
(Wieso?). Der folgende Fakt sagt uns, nach wie vielen Wurzeln wir suchen.
Fakt
Ein Polynom vom Grad [latex]n[/latex] besitzt höchstens [latex]n[/latex] Nullstellen[1].
Beweis
Diese Tatsache zeigt man mit Hilfe der Polynomdivision. (Wenn Sie dies im Detail interessiert, lesen Sie zum Beispiel Arens [2].) ∎
Die Zahl [latex]z_{0}[/latex] kann also höchstens [latex]n[/latex] verschiedene Wurzeln haben. Mit der Polardarstellung können wir sie leicht finden. Dazu sei [latex]z_{0}=r_{0}e^{i\theta _{0}}[/latex] die Polardarstellung von [latex]z_{0}[/latex]. Wenn [latex]w=re^{i\varphi }[/latex] eine [latex]n[/latex]-te Wurzel von [latex]z_{0}[/latex] ist, dann gilt
[latex]\begin{aligned}[]w^{n}=r^{n}e^{in\varphi }=z_{0}=r_{0}e^{i\theta _{0}}.\label{eq:wurzelEQ-1}\end{aligned}[/latex]
Wenn wir nicht vorsichtig sind, denken wir, dass sich aus (4.7)
bzw.
ergibt.
Wo sind die anderen Wurzeln? Um diese zu finden, müssen wir uns einfach in Erinnerung rufen, dass der Polarwinkel bis auf ein Vielfaches von [latex]2\pi[/latex] definiert ist. Daher folgt aus (4.7), dass
bzw.
Das heisst, jede komplexe Zahl
[latex]\begin{aligned}[]w_{k}=\sqrt [n]{r_{0}}e^{i\left (\frac {\theta _{0}}{n}+\frac {2\pi k}{n}\right )}\label{eq:W_k erste mal-1}\end{aligned}[/latex]
ist eine [latex]n[/latex]-te Wurzel von [latex]z_{0}[/latex].
Das ist aber ein bisschen seltsam, oder? Statt einer Wurzel haben wir jetzt unendliche viele? Laut Fakt können wir höchstens [latex]n[/latex] Wurzeln haben. Die Lösung dieses Geheimnisses liegt nochmals in der Tatsache, dass der Polarwinkel nur bis auf ein Vielfaches von [latex]2\pi[/latex] definiert ist. Der Lesbarkeit halber schreiben wir (4.8) mit [latex]\exp[/latex] statt mit [latex]e[/latex]:
Schauen wir uns die Zahlen genauer an. Alle [latex]w_{k}[/latex] haben den selben Betrag [latex]\sqrt [n]{r_{0}}[/latex], aber ihre Polarwinkel unterscheiden sich voneinander mit einem Vielfachen von [latex]\frac {2\pi }{n}[/latex]. Das weist daraufhin, dass [latex]w_{k}=w_{k+n}[/latex], und so ist es in der Tat.
Ausserdem sind die Wurzeln [latex]w_{0},w_{1},\cdots ,w_{n-1}[/latex] alle unterschiedlich voneinander. Aus obigem Fakt wissen wir, dass es keine anderen gibt.
Wir fassen diese Diskussion zusammen:
Die [latex]n[/latex]-ten Wurzeln von [latex]z_{0}=r_{0}e^{i\theta _{0}}[/latex] sind genau
für [latex]k=0,1,\dots ,n-1[/latex].
Beispiel
Bestimmen Sie die dritten Wurzeln von [latex]-8[/latex] in Polar- und Normalform.
Lösung:
Um das Kochrezept oben zu verwenden, müssen wir zuerst die Polardarstellung von [latex]-8[/latex] bestimmen. Der Betrag ist
und der Winkel ist [latex]\pi[/latex]. Das heisst
Damit ergeben sich nach dem obigen Rezept die dritten Wurzeln wie folgt:
In Normalform
Wir sehen, dass [latex]w_{1}[/latex] eine reelle Wurzel ist.
4.9.1 – Wie sieht das geometrisch aus?
Wir haben oben ein Kochrezept für alle [latex]n[/latex]-ten Wurzeln einer gegebenen komplexen Zahl [latex]z_{0}=r_{0}e^{i\theta _{0}}[/latex] hergeleitet. Als Nächstes zeichnen wir diese in die komplexe Ebene ein und sehen, welche geometrischen Eigenschaften sich herausstellen. Zuerst bemerken wir, dass der Betrag aller Wurzeln gleich ist: Er ist [latex]\sqrt [n]{r_{0}}[/latex]. Das heisst, dass alle Wurzeln auf einem Kreis mit Radius [latex]\sqrt [n]{r_{0}}[/latex] liegen.
Zweitens betrachten wir ihre Winkel. Eine Wurzel hat den Winkel [latex]\frac {\theta _{0}}{n}[/latex] und die anderen Wurzeln sind jeweils um den Winkel [latex]\frac {2\pi }{n}[/latex] versetzt.
Um die [latex]n[/latex]-te Wurzel einer Zahl [latex]z_{0}=r_{0}e^{i\theta _{0}}[/latex] zu zeichnen, müssen wir also eine Wurzel mit Betrag [latex]\sqrt [n]{r_{0}}[/latex] und Winkel [latex]\frac {\theta _{0}}{n}[/latex] zeichnen und dann diese Wurzel so oft um den Winkel [latex]\frac {2\pi }{n}[/latex] versetzen, bis wir zurückkommen zur ersten Wurzel.
Spielen Sie mit diesem Applet, um das eben Erklärte nachzuvollziehen.
Beispiel
Finden Sie alle Lösungen von [latex]z^{8}=4+3i.[/latex] Zeichnen Sie diese in die komplexe Ebene ein.
Lösung:
Die Lösungen sind genau die acht Wurzeln von [latex]4+3i[/latex]. Also ist diese Aufgabe äquivalent zu: «Finden Sie die acht Wurzeln von [latex]4+3i[/latex]«.
Um das obige Rezept zu verwenden, müssen wir zuerst die Polardarstellung von [latex]4+3i[/latex] finden. Dazu berechnen wir
Da diese Zahl im ersten Quadranten liegt, berechnet sich ihr Winkel gemäss
(Man kann den Wert von [latex]\theta _{0}[/latex] mit einem Taschenrechner berechnen.) Mit diesen Informationen können wir schreiben
Laut der geometrischen Beschreibung ist nun die Lösung der Aufgabe sehr einfach zu zeichnen. Zuerst zeichnen wir die Wurzel mit dem Winkel [latex]{\displaystyle \frac {\theta _{0}}{8}}[/latex] und Betrag [latex]{\displaystyle \sqrt [8]{5}}.[/latex] In der Abbildung unten ist [latex]z_0[/latex] blau eingezeichnet, rot sind die Wurzeln eingezeichnet.

Des Weitern haben wir noch sieben andere Wurzeln, jede um [latex]{\displaystyle \frac {2\pi }{8}}[/latex] versetzt. Alle Wurzeln haben denselben Betrag.
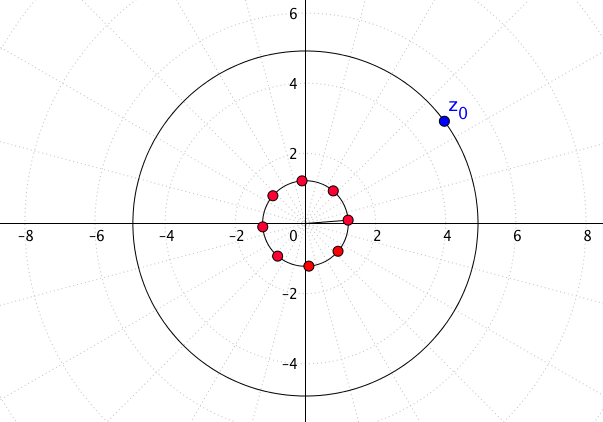
Algebraisch sind die Wurzeln gleich
Um diese «Versetzung» algebraisch zu sehen, können wir das obige Resultat so umschreiben:
Bemerkung
Um den letzten Schritt der obigen Lösung zu verstehen, kann sich der Leser daran erinnern, was die Multiplikation mit einer Zahl der Form [latex]e^{i\phi }[/latex] bedeutet. Siehe Abschnitt 4.6.
Beispiel
Die Lösungen von
[latex]\begin{aligned}[]z^{n}=1\label{eq:EinheitsW-1}\end{aligned}[/latex]
nennt man [latex]n[/latex]-te Einheitswurzel. Berechnen und zeichnen Sie alle [latex]n[/latex]-ten Einheitswurzeln für [latex]n=2,3,4,5,6[/latex].
Lösung:
Das ist leicht geometrisch gemacht. Die Polardarstellung von [latex]1=1+0i[/latex] ist sehr einfach. Sie ist [latex]1=1e^{i\cdot 0}.[/latex] Deshalb ist eine [latex]n[/latex]-te Wurzel gleich
Das ist keine Überraschung. [latex]1[/latex] ist immer eine Lösung von 4.9, da [latex]1^{n}=1[/latex]. Die anderen Wurzeln sind um den Winkel [latex]{\displaystyle \frac {2\pi }{n}}[/latex] versetzt. Das heisst, dass alle Lösungen auf dem Einheitskreis liegen und jeweils den Winkel [latex]{\displaystyle \frac {2\pi k}{n}}[/latex] haben, [latex]\quad k=0,\cdots ,n-1.[/latex]
Für [latex]n=2[/latex] bekommen wir
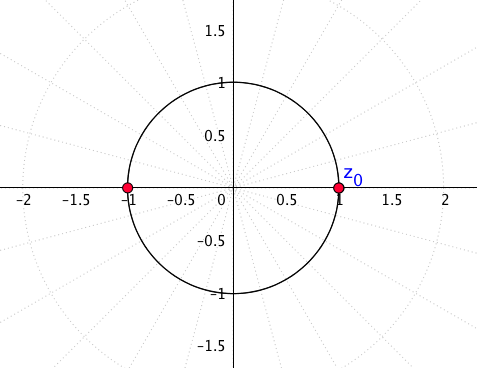
Für [latex]n=3[/latex]
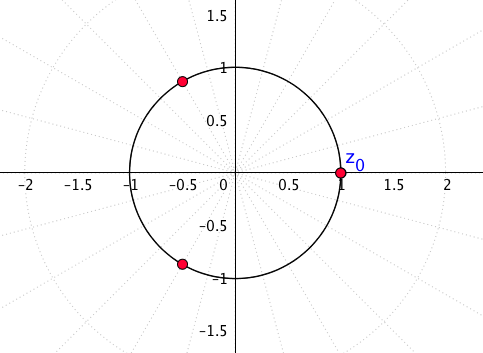
Zum Beispiel sind hier die Einheitswurzeln mit [latex]n=6[/latex]:
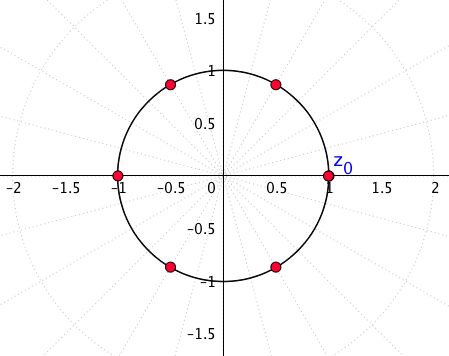
Für ein anderes [latex]n[/latex] können Sie die Wurzeln in diesem Applet sehen.
4.9.2 – Quadratwurzeln
Beispiel
In diesem Beispiel zeigen wir zwei äquivalente Wege, quadratische Wurzeln einer komplexen Zahl zu schreiben. Im Gegensatz zum reellen Fall[3] gibt es keine eindeutige Bedeutung von [latex]\sqrt {z}[/latex] wenn [latex]z\in \mathbb {C}\setminus \mathbb {R}[/latex]. Es gibt immer zwei quadratische Wurzeln, von denen keine bevorzugt wird. Diese Wurzeln können wir natürlich mit dem obigen Rezept finden.
Sei [latex]z\in \mathbb {C}[/latex], [latex]z=re^{\theta i}[/latex], [latex]r\geq 0[/latex]. Laut dem Rezept oben, sind
die quadratischen Wurzel von [latex]z[/latex]. Ausdrücklich sind sie
Da [latex]e^{\pi i}=-1[/latex] und [latex]w_{2}=w_{1}e^{\pi i}[/latex], gilt
wie erwartet. Das heisst, um die Quadratwurzeln zu finden, reicht es, eine Wurzel zu finden und für die andere das Vorzeichen zu ändern. Daher können wir die Wurzeln folgendermassen schreiben
und diese Schreibweise sieht ähnlich aus wie im reellen Fall.
Korollar
Die Lösungen einer quadratischen Gleichung [latex]az^{2}+bz+c=0,[/latex] [latex]a,b,c\in \mathbb {C}[/latex] sind
wobei [latex]\sqrt {b^{2}-4ac}[/latex] eine (egal welche) der zwei Wurzeln von [latex]b^{2}-4ac[/latex] ist. Diese Formel gilt, egal ob [latex]b^{2}-4ac[/latex] eine reelle oder komplexe Zahl ist.
Anders gesagt, die Lösungen sind
wobei [latex]w_{1}[/latex] und [latex]w_{2}[/latex] die zwei Wurzeln von [latex]b^{2}-4ac[/latex] sind.
Achtung: Es kann selbstverständlich auch der Fall eintreten, dass gilt [latex]b^{2}-4ac =0[/latex]. In diesem Fall sind die beiden Lösungen der quadratischen Gleichung identisch. Betrachten Sie dazu das Beispiel [latex]z^{2}-4z+4=0.[/latex] Hier ist [latex]z=2[/latex] eine doppelte Nullstelle.
Bemerkung
Oben verwenden wir die Gleichheit
Diese nennt man «die Euler’sche Identität» und einige Leute auch «die schönste Identität der Mathematik», und die formen Sie folgendermassen um:
Warum die Schönste? Vielleicht weil sie sehr verschiedene Sachen miteinander verbindet. Wir haben die Grundrechenarten Addition und Potenzen.
Weiter verbindet sie wichtige Konstante: [latex]1[/latex] und [latex]0[/latex] kommen aus der Arithmetik, die Kreiszahl [latex]\pi[/latex] kommt aus der Geometrie, die imaginäre Zahl [latex]i[/latex] kommt aus der Algebra, die konstante Zahl [latex]e[/latex] kommt aus der Analysis/Wahrscheinlichkeitsrechnung. Und diese Identität verbindet wirklich alles! Eine erheiternde Erläuterung der Eulerschen Identität finden Sie im abschliessenden Video unten
- Bemerkung: Aus dem Gymnasium sind sich einige Studenten daran gewöhnt, dass mit "Nullstellen" die Schnittmenge des Graphen mit der reellen Achse gemeint ist. Das gilt aber nur für reelle Funktionen. Hier sprechen wir über Polynome (deren Koeffizienten komplexe Zahlen sind) und Lösungen von Polynomgleichungen, die auch komplexe Zahlen sind. Also ist diese Vorstellung von Nullstellen als Schnittmenge mit der reelle Achse hier unpassend. ↵
- Arens, Tilo and Hettlich, Frank and Karpfinger, Christian and Kockelkorn, Ulrich and Lichtenegger, Klaus and Stachel, Hellmuth: Mathematik (Springer-Verlag, 2015) ↵
- Wenn [latex]r\in \mathbb {R}[/latex] ist, dann ist [latex]\sqrt {r}[/latex] nicht definiert, wenn [latex]r\lt 0[/latex], oder [latex]\sqrt {r}[/latex] ist die (eindeutig definierte) nicht-negative, reelle Zahl, deren Quadrat [latex]r[/latex] ist. ↵