Zur Beschreibung mit welchen Raten unsere zwei Proteine [latex]A[/latex] und [latex]R[/latex] gebildet werden, haben wir zwei Differentialgleichungen [latex]I[/latex] und [latex]II[/latex] gefunden:

Dies ist ein nicht lineares [latex]2 \times 2[/latex]-DGL-System mit zwei DGL und zwei Funktionen [latex]A: t \mapsto A(t)[/latex] und  [latex]R: t \mapsto R(t)[/latex]. In der Regel lassen sich solche Systeme nur in Spezialfällen exakt lösen. Eine exakte Lösung bedeutet, dass man für die Lösungsfunktionen [latex]A[/latex] und [latex]R[/latex] explizite Ausdrücke für [latex]A(t)[/latex] und [latex]R(t)[/latex] angeben kann. Das Problem liegt vor allem darin, dass die beiden DGL (nicht linear) gekoppelt sind: Um die DGL für [latex]A[/latex] zu lösen, müssen wir [latex]R[/latex] kennen und vice versa.

Die folgenden Ausführungen erfordern ein mathematisches Verständnis, das über Grundlagen hinausreicht.

8.2 – Stationäre Lösungen des Systems

Auch wenn wir in der Regel keine expliziten Ausdrücke für die Lösungen [latex]A(t)[/latex] und [latex]R(t)[/latex] finden werden, ist die Suche nach stationären Lösungen des Systems meist erfolgreich. Wie im eindimenstionalen Fall in Kapitel 4 zeichnen sich diese Lösungen dadurch aus, dass das System im Gleichgewicht ist. Auch hier wollen wir unten untersuchen, was bei einer Störung des Gleichgewichts passiert, wir also in der Nähe einer stationären Lösung starten.

Stationäre Lösungen sind Lösungen [latex]A_\infty[/latex] und [latex]R_\infty[/latex] mit \[\begin{pmatrix}R’_\infty \\A’_\infty \end{pmatrix} =\begin{pmatrix}0 \\0 \end{pmatrix} =\begin{pmatrix}m_R\cdot\beta_R\cdot\frac{K_A\cdot A_\infty}{1+K_A\cdot A_\infty}-\frac{R_\infty}{\tau_R} \\m_A\cdot\beta_A\cdot\frac{1}{1+K_R\cdot R_\infty}-\frac{A_\infty}{\tau_A} \end{pmatrix}.\]

Die Gleichung [latex]II[/latex]  können wir nach [latex]A_\infty[/latex] auflösen und erhalten mit der Notation  [latex]C_A = m_A \cdot \beta_A \cdot \tau_A[/latex]

\[A_\infty = \dfrac{ m_A \cdot \beta_A \cdot \tau_A}{1 + K_R \cdot R_\infty} = \dfrac{ C_A}{1 + K_R \cdot R_\infty}. \]

Suche [latex]R_\infty[/latex]

Dieses [latex]A_\infty[/latex] setzen wir in die erste Gleichung [latex]I[/latex] ein. Durch elementare Rechnungen ergibt sich für [latex]R_\infty[/latex] die Quadratische Gleichung mit der weiteren Notation  [latex]C_R = m_R \cdot \beta_R \cdot \tau_R[/latex]
\[R_\infty^2 + \frac{K_A \cdot C_A + 1}{K_R} \cdot R_\infty – \frac{K_A}{K_R} \cdot C_A \cdot C_R = 0.\]

Dies Gleichung hat abhängig von den Konstanten zwei Lösungen [latex]R_{\infty,1} \neq R_{\infty,2}[/latex], genau eine Lösung [latex]R_{\infty,1} = R_{\infty,2}[/latex] oder keine Lösung. In der Regel wird es zwei Lösungen [latex]R_{\infty,1} \neq R_{\infty,2}[/latex] geben, aber was bedeutet es, wenn dies nicht der Fall ist? Kann das biologisch passieren?

Mit [latex]A_\infty = \dfrac{ C_A}{1 + K_R \cdot R_\infty}[/latex] und Einsetzen der allfälligen Lösungen [latex]R_\infty[/latex] oben erhalten wir die stationäre Lösungen [latex]\begin{pmatrix}R_\infty \\A_\infty \end{pmatrix}[/latex].

Geometrische Suche

Um die Lage der Fixpunkte in Abhängigkeit der Konstanten zu erkennen, lässt sich auch wie folgt vorgehen:

1. Löse beide Gleichung [latex]I  = 0 = II[/latex] nach [latex]A[/latex] auf. Das ergibt zwei Funktionen [latex]f_{1/2}: R \mapsto f_{1/2}(R)[/latex].
2. Plotte die Graphen der Funktionen [latex]f_{1/2}[/latex] für unterschiedliche Konstanten in ein [latex](R, A)[/latex] – Koordinatensystem.
3. Allfällige Schnittpunkte sind stationäre Lösungen [latex]\begin{pmatrix}R_\infty \\A_\infty \end{pmatrix}[/latex].

Stabilität stationärer Lösungen

Analog zu den Differentialgleichungen können wir uns fragen, wie die Lösungen in der Nähe eines Fixpunktes aussehen. Bei der Vorstellung des Vorgehens wählen wir für eine bessere Übersicht die Konstanten gleich [latex]1[/latex]. Die Quadratische Gleichung oben vereinfacht sich zu [latex]R_\infty^2 + 2 \cdot R_\infty - 1 = 0[/latex] mit den Lösungen [latex]R_{\infty,1/2} = - 1 \pm \sqrt{2}[/latex].

Linearisierung mit vereinfachten Konstanten

Jetzt wird das System aus nicht linearen DGL in der Nähe eines Fixpunktes linearisiert. Dafür brauchen wir die Jacobi-Matrix, die sich aus partiellen Ableitungen der Funktionen [latex]F_1[/latex] und [latex]F_2[/latex] zusammensetzt mit [latex]F_1(R,A) = \dfrac A{1+A} - R[/latex] und [latex]F_2(R,A) = \dfrac 1{1+R} - A[/latex].

Dann ist [latex]\begin{pmatrix} \frac{\partial F_1}{\partial R} & \frac{\partial F_1}{\partial A}  \\\frac{\partial F_2}{\partial R} & \frac{\partial F_2}{\partial A}\end{pmatrix} =\begin{pmatrix} -1 &\frac{1}{(1+A)^2} \\ - \frac{1}{(1+R)^2} & -1 \end{pmatrix}.[/latex] Hier setzen wir den Fixpunkt [latex]\left (R, \frac 1{1+R}\right) = \left(- 1 \pm \sqrt{2}, \frac 1{\sqrt 2}\right )[/latex] mit positiven Koordinaten ein und erhalten [latex]\begin{pmatrix} -1 &\frac{1}{3 + \sqrt2 } \\ - \frac{1}{2} & -1 \end{pmatrix}.[/latex] Diese Matrix hat eine positive Determinante und eine negative Spur [latex]= -2[/latex]. Damit haben die Eigenwerte der Matrix einen negativen Realteil und der Fixpunkt ist stabil (attraktiv). Eine Lösung, die in der Nähe der stationären Lösung startet, wird sich dieser im Laufe der Zeit annähern.

Linearisierung allgemein

Um die Rechnungen mit den Konstanten zielführend zu gestalten, sollte biologisch entschieden werden, wie diese (in einer vereinfachten aber sinnvollen Annahme) gewählt werden können. Dann kann die gleiche Prozedur durchgeführt werden.

8.3 – Numerische Lösungen

Für eine numerische Lösung wählen wir geeignete und realitätsnahe Werte für die Konstanten und Anfangswerte. Zum Beispiel

• [latex]\tau_R, \tau_A:   10 - 10^5 s[/latex]
• [latex]k_{on}, k_{off}:  10^6 - 10^8 s^{-1}M^{-1}[/latex]
• [latex][R_0]:  10^{-10} M[/latex]
• [latex][A_0]:  10^{-9} - 10^{-5} M[/latex]
• [latex]m_R, m_A : 10 - 100[/latex] Kopien des Proteins pro mRNA
• [latex]\beta_R, \beta_A: 0.1 - 0.9[/latex]

Mit Hilfe von diesen Bereichen der Konstanten wurden mit dem ode45 in Matlab die Differenzialgleichungen numerisch gelöst. Auf eine theoretische Abhandlung, wie das numerische Lösungsverfahren ode45 funktioniert, wird im Rahmen dieses Projekts verzichtet. Schauen wir uns aber an, was mit den Konzentrationen der beiden Proteine passiert, seien folgende Anfangswerte gegeben:

[latex][A_0]=10^{-6}M, [R_0]=0\,M.[/latex]

Es wurde mit zwei Parametersets die numerische Lösung berechnet, um Einflüsse dieser Parameter zu sehen. In beiden Fällen waren [latex]m_A=25 Proteine/mRNA[/latex]; [latex]m_R=5 Proteine/mRNA[/latex]; [latex]\beta_A=0.8[/latex], [latex]\beta_R=0.3[/latex], [latex]K_R=30[/latex], [latex]\tau_A=50\,s[/latex], [latex]\tau_R=10\,s[/latex]. Nur [latex]K_A[/latex] wurde verändert und zwar im ersten Fall (Abbildung (a)) gilt [latex]K_A=150[/latex] und im zweiten Fall gilt [latex]K_A=0.1[/latex] (Abbildung (b)). Beide numerischen Lösungen wurden über den Zeitraum [latex][0,100][/latex] Sekunden beobachtet.

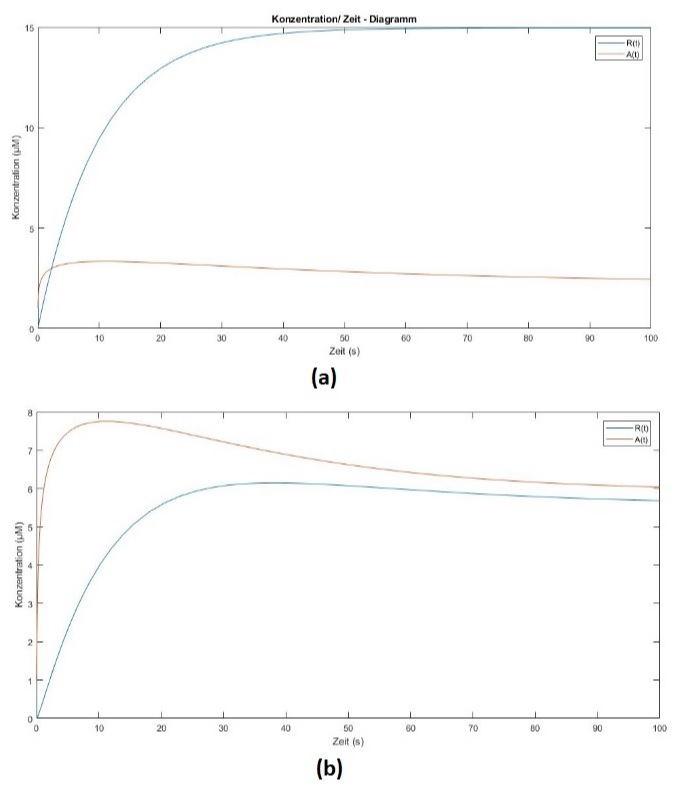
Abbildung 8.1 – Numerische Lösungen des Differentialgleichungssystem mit verschiedenen Parametern. (a): Parameter [latex]K_A=150[/latex] führt zu höherer Konzentration von R(t). Ein typischer Verlauf ist nur bei A(t) festzustellen. (b): Parameter [latex]K_A=0.1[/latex]. Führt zu ähnlichen Gleichgewichtskonzentrationen bei den Proteinen und ein charakteristischer Verlauf ist bei beiden Kurven festzustellen.

Beobachten wir das Verhalten der Kurven von [latex]A(t)[/latex] und [latex]R(T)[/latex]: Da wir annehmen, dass es zu Beginn keinen Repressor gibt ([latex]R(0)=0[/latex]), steigt die Kurve schnell an. Die Syntheserate von [latex]A[/latex] nimmt aber mit steigender Konzentration von [latex]R[/latex] ab.  Man erkennt, dass die Kurven einen unterschiedlichen Verlauf haben. Falls es den Repressor nicht geben würde, wäre die Konzentrationskurve von [latex]A(t)[/latex] von der Form wie die Kurve [latex]R(t)[/latex] in Abbildung (a). Man erkennt, dass diese Kurve zeitlich viel länger braucht, um in die Nähe des Gleichgewichts zu kommen. Dies ist aber für die gewünschte Wirkung des Enzyms unerlässlich, sodass es möglichst schnell seine Wirkung erzielen kann. Die Veränderung des Parameters [latex]K_A[/latex] zeigt, dass die Einstellung des Gleichgewichts für die Proteinkonzentration [latex]A[/latex] gleich schnell ist. Jedoch wird bei (a) viel mehr Protein [latex]R[/latex] produziert, was für die Zelle unvorteilhaft ist, da sie viel Energie aufwenden muss und toxische Wirkungen von hohen Proteinkonzentrationen auftreten können. Fall (b) ist aus diesem Blickwinkel viel günstiger. Sowohl A und R haben ähnliche Gleichgewichtskonzentrationen.

Bis jetzt haben wir immer angenommen, dass die Konzentration des Repressorproteins niedrig ist. Die Zelle möchte normalerweise nicht zu hohe Konzentrationen haben. Wie würde dies aber aussehen, wenn zu Beginn die Repressorproteinkonzentration hoch ist. Es wurde mit den gleichen Werten für die Parameter, sowie [latex]K_A=0.1[/latex] und [latex]R(0)=20\cdot 10^{-6}\,M[/latex] gearbeitet (siehe Abbildung 8.2).

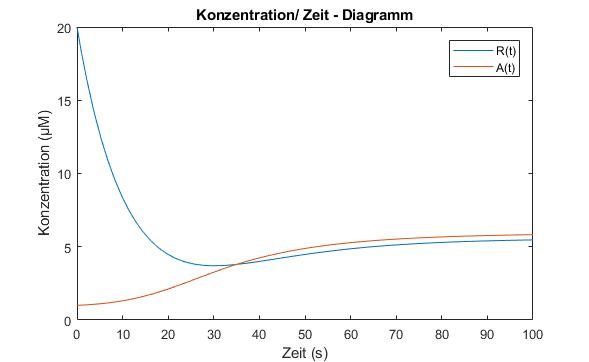
Abbildung 8.2 – Numerische Lösung des Differentialgleichungssystem mit einer hohen Startkonzentration des Repressorproteins R.

Im Vergleich zu Abbildung 8.1 (b) braucht es viel länger, bis die Konzentration von [latex]A[/latex] in die Nähe der Gleichgewichtskonzentration kommt. In diesem Fall braucht es ca. 50 Sekunden, im Fall [latex]R(0)=0\,M[/latex] braucht es nur ca. 10 Sekunden. Dies kommt dadurch zustande, dass die hohe Konzentration von R die Bildung von A inhibiert.

Sind die Ergebnisse jetzt repräsentativ für eine biologische Zelle? In einer Zelle wären Proteinkonzentrationen näherungsweise im Gleichgewicht. Numerische Lösungen, bei der die Startkonzentrationen in der Nähe der Gleichgewichtskonzentrationen sind, zeigen, dass sie sehr schnell das Gleichgewicht erreichen. Auf der anderen Seite ist dieser schnelle Zeitaspekt ein Problem des Modells, denn es vergeht Zeit von der Bindung der Polymerase bis zur Proteinherstellung. Da das Ribosom nur 10-20 Aminosäuren pro Sekunde verknüpfen kann, die RNA-Polymerase ca. 50 Nucleotide pro Sekunde, braucht es für die Genexpression eines 1000 Nucleotid langen Gens 20 Sekunden in Bakterien. Bei Eukaryonten ca. 1 Minute. Diese Zeit wurde in unserem Modell nicht miteinberechnet, hätte aber einen grossen Einfluss, da nach 20 Sekunden schon viel Protein hergestellt werden wurde (Abbildung 8.1). Dies müsste in einem nächsten Schritt verfeinert werden, in dem man bei beiden Proteinen eine solche Wartezeit einbaut, bis es aktiv wird.

8.4 – Erkenntnisse aus der Simulation

Zusammenfassend kann man sagen, dass durch die numerische Lösung unseres Modells einige interessante Beobachtungen gemacht wurden. Hohe Konzentrationen führen zu einer Verzögerung des Einstellens des Gleichgewichts, das Gleichgewicht wird durch den Repressor schneller erreicht als ohne Repressor und die Kurvenform ist abhängig von den Parametern. Solche Beobachtungen hätten nicht ohne weiteres gemacht werden können. Jedoch hat das Modell auch noch einige Schwächen, wie die Beachtung der Zeitgrösse der Proteinherstellung.