5.1 – Komplexbildung
Durch das Binden von Proteinen an die DNA bilden sich Komplexe. In unserem Fall bindet das Protein [latex]A[/latex] am Promotor [latex]p_R[/latex] eines Gens [latex]R[/latex]. Sind das Protein A und der Promotor [latex]P_R[/latex] gebunden, sprechen wir von [latex]A:P_R[/latex]. In unserem Modell ist das Protein [latex]A[/latex] ein Aktivator und die Komplexbildung führt zur Genexpression, der aktive Komplex wird mit [latex](A:P_R)_{aktiv}[/latex] bezeichnet. Die Komplexbildung bzw. -dissoziation lässt sich dann wie folgt formulieren:
\[A+P_R\rightleftharpoons A:P_R\]
Um die Geschwindigkeit des Prozess zu beschreiben, benötigen wir neben der Geschwindigkeitskonstante die Konzentrationen der ungebundenen Promotoren und die der Proteine. Schliesslich würden fehlende Proteine oder bereits gebundene Promotoren die Bildung neuer Komplexe einschränken.
Betrachten wir andererseits die Dissoziation, so benötigen wir die Konzentrationen der bestehenden Komplexe.
Im chemischen Gleichgewicht bilden sich Komplexe gleich schnell wie sie dissoziieren. Somit kann die Geschwindigkeit der Komplexbildung mit derjenigen der Komplexdissoziation gleichgesetzt werden und es gilt:
\[k_{on}\cdot [A][P_R]=k_{off}\cdot [A:P_R]\]
Durch Umformen lässt sich die Konzentration der Komplexe berechnen.
Wir nehmen vorübergehend an, dass die Konzentration des Proteins [latex]A[/latex] konstant ist. Dies aus folgender Überlegung: Unserem Modell nach ist das Protein [latex]A[/latex] ein Aktivator. Durch das Binden am Promotor des Gen R, wird das Protein R produziert, welches daraufhin als Repressor von A wirkt. Da wir uns an dieser Stelle aber erst bei der Komplexbildung befinden, haben wir in unserer Vereinfachung kein Protein R, welches die Konzentration des Proteins [latex]A[/latex] reduzieren kann.
Wie können wir nun die Konzentration des Promotors berechnen? Die meisten Bakterien besitzen nur ein Chromosom und sind ausserhalb der Zellteilung haploid. Sie haben entsprechend auch nur eine Kopie jedes Chromosomes. Prokaryoten besitzen ebenfalls kaum copy number variations (CNVs) und haben somit meistens nur ein Promotor pro Zelle. In unserem Modell werden wir also eine konstante Anzahl an Promotoren annehmen. Allerdings besitzen Prokaryoten auch die Fähigkeit, zusätzliche DNA in Form von Plasmiden zu speichern und diese zum Teil gegenseitig auszutauschen. Dadurch gebe es also Variationen in der Menge DNA. Für unser Modell schliessen wir solche Möglichkeiten aber aus. Bei eukaryotischen Zellen können eine unterschiedliche Anzahl an gleichen Genen im Genom vorkommen und auch mehrfache Chromosomensätze sind möglich.
Das Ziel folgender Rechnung ist, dass wir das Verhältnis von gebundenen Promotoren zur Gesamtanzahl Promotoren mit Hilfe der Konzentration des Proteins A bestimmen. Wir können die Gesamtmenge der Promotoren in freie und gebundene Promotoren unterteilen:
\[ [P_R^{total}]=[P_R]+[A:P_R] \implies [P_R] = [P_R^{total}] – [A:P_R] \]
Einsetzen in die Gleichung (*) liefert mit ein wenig Umformen:
\[\frac{[A:P_R]}{[P_R^{total}]}=\frac{K_A\cdot [A]}{1+K_A\cdot [A]}\]
Wodurch wir das Verhältnis zwischen gebundenen Promotoren und der Gesamtzahl Promotoren erhalten. Dies beschreibt dementsprechend die Wahrscheinlichkeit, dass ein Promotor gebunden ist.
Bei [latex][A]=\frac{1}{K_A}[/latex] sind beispielsweise genau 50% der Promotoren gebunden. Die Gleichgewichtskonstante von Promotoren liegt vorwiegend im Bereich von ca. 1-1000 nM.
Mit Hilfe der Thermodynamik kann [latex]K_A[/latex] aus der Gleichung [latex]\Delta G=-RT\ln(K_A)[/latex] bestimmt werden.
Um [latex]K_A[/latex] aus dieser Gleichung zu erhalten, brauchen wir allerdings zusätzliche Angaben. Offen steht nämlich die Differenz zwischen den zwei Gibbs-Energien der zwei Systeme [latex]G[/latex] und die Temperatur [latex]T[/latex], bei welcher die Reaktion stattfindet. Die Gibbs-Energie eines Systems ergibt sich wiederum aus dessen Temperatur [latex]T[/latex], sowie dessen Entropie [latex]S[/latex] und Enthalpie [latex]H[/latex] mit [latex]G = H - TS[/latex]. Da [latex]\Delta G[/latex] von den meisten Reaktionen bekannt ist, kann dadurch die Gleichgewichtskonstante bestimmt bzw. für unser Modell abgeschätzt werden.
5.2 – Dynamik
Da uns die Konzentration der Komplexe für die Genexpression von R wichtig scheint, wollen wir erst einmal untersuchen, wie sie sich diese im Laufe der Zeit entwickelt. Hierfür verwenden wir Differentialgleichungen, wie im vorherigen Kapitel beschrieben.
Die Veränderung lässt sich dabei einfach aus der Differenz zwischen gebildeten und dissoziierten Komplexen berechnen. Daraus entsteht folgende Gleichung:
\[\frac{d[A:P_R]}{dt}=k_{on}[A][P_R]-k_{off}[A:P_R]=k_{on}[A](([P_R^{total}]-[A:P_R])-k_{off}[A:P_R])\]
\[\frac{d[A:P_R]}{dt}=\underbrace{-(k_{on}[A]+k_{off})}_a[A:P_R]+\underbrace{k_{on}[A][P_R^{total}]}_{b}.\]
Es ist also eine DGL der Art [latex]f'(t)=a\cdot f(t)+b[/latex] mit konstanten Koeffizienten [latex]a[/latex] und [latex]b[/latex].
Dass [A] konstant ist, ist gerechtfertigt, da der Zeitraum noch so klein ist, dass kein [latex]R[/latex] gebildet wurde. Wir betrachten also nur einen kurzen Abschnitt der Reaktion.
Wir sind interessiert an der Lösung der Differenzialgleichung [latex]f'=af+b[/latex]. Dies haben wir im Kapitel 4 diskutiert.
Mit dem Startwert [latex]f(0)=N_0[/latex] ist die Lösung [latex]\displaystyle f(t)=N_0\cdot e^{at}+-\frac{b}{a}(1-e^{at}).[/latex]
Für die Eindeutigkeit brauchen wir einen Startwert [latex]N_0[/latex] . Wie im Kapitel 2.2.1 beschrieben sind Zellen sparsam und produzieren nur zu bestimmten Zeitpunkten notwendige Proteine. Hergestellte Proteine haben zudem nur eine begrenzte Lebensdauer. Wir nehmen der Einfachheit an, dass wir uns am Anfang des Prozesses der Komplexbildung befinden und es noch keine Komplexe [latex](A:P_R)_{aktiv}[/latex] gibt. Somit können wir [latex]N_0=0[/latex] setzen und es ergibt sich: [latex]\displaystyle f(t)=-\frac{b}{a}(1-e^{at}).[/latex]
Werden [latex]a[/latex] und [latex]b[/latex] wieder eingesetzt, ergibt sich:
\[ [A:P_R](t)=\underbrace{\frac{K_A[A]}{1+K_A[A]}[P_R^{total}]}_{[A:P_R]_{\infty}}(1-e^{-(k_{on}A]+k_{off})\cdot t})\]
Da [latex]a[/latex] negativ ist und [latex]b[/latex] positiv, ergibt sich die positive stationäre Lösung
\[ [A:P_R]_\infty=[P_R^{total}]\frac{K_A[A]}{1+K_A[A]}>0\]
Wir haben ein beschränktes Wachstum mit Kapazität [latex]\kappa = [A:P_R]_\infty=[P_R^{total}]\frac{K_A[A]}{1+K_A[A]}>0[/latex] und Verlauf wie hier gezeigt:
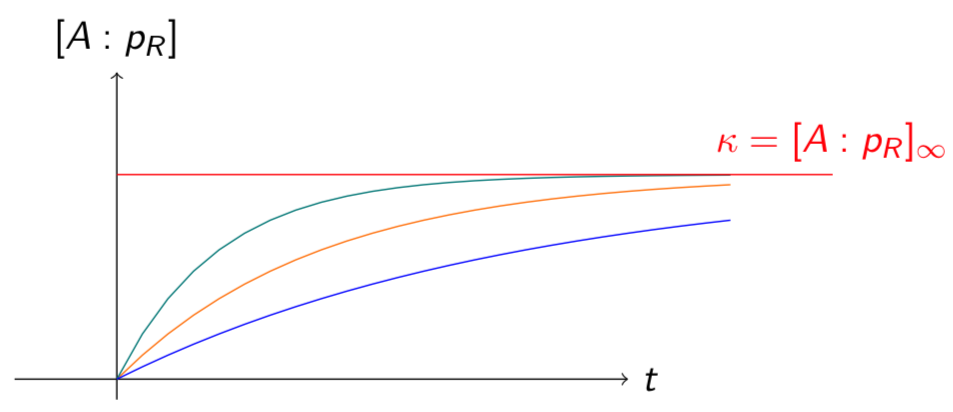
Abbildung 5.1 – Verlauf der Komplexbildung von Protein A mit Promotor PR mit verschiedenen kon-und koff-Werten bei gleichbleibender Kapazität. Es dauert nur wenige Millisekunden, bis das Gleichgewicht näherungsweise erreicht ist.
Die Kapazität aktivierter – in diesem Fall gebundener – Promotoren ist für den weiteren Verlauf des Proteinzyklus interessant, denn die Kapazität wird bei der Synthese der Proteins R ein limitierender Faktor sein. Dementsprechend führen beispielsweise geringe Mengen gebundener Komplexe dazu, dass die Genexpression von R nicht im grossen Masse stattfindet.
Zusätzlich lässt sich daraus aber auch erkennen, dass die Kapazität aktivierter Promotoren von der Konzentration des Proteins A abhängt. Im späteren Verlauf wird diese nach der Genexpression von R aufgrund des negativen Feedbacks abnehmen. Dies führt dazu, dass auch die Kapazität der Komplexe kleiner wird, was sich daraufhin negativ auf die Aktivierung der Genexpression von R auswirkt.
Diese mathematische Interpretation entspricht genau dem beschriebenen Mechanismus des negativen Feedbacks im Kapitel 2.2.1.
Wichtig anzumerken ist an dieser Stelle allerdings auch, dass die Komplexbildung ein schneller Prozess ist. Sie geschieht im Bereich von Millisekunden. Im Vergleich dazu stehen die Transkription und die Translation, welche beide sekunden- bis minutenlang dauern und somit deutlich langsamer ablaufen als die Komplexbildung. Auf dieser Zeitskala wird die Kapazität aktivierter Promotoren äusserst schnell erreicht, weshalb die Komplexbildung letztendlich im Proteinzyklus zeitlich kaum ins Gewicht fällt. Somit wird bei den nächsten Kapiteln als Konzentration des Promotorkomplexes [latex](A:P_R)_{aktiv}[/latex] nur noch der Wert [latex]\kappa[/latex] verwendet, da wir annehmen, dass sich das Gleichgewicht eingestellt hat. Somit ist auch die Annahme [latex][A:P_R](0)=0[/latex] hinfällig.