4.1 – Folgerungen aus dem System

Aus unseren Überlegungen lassen sich folgende Schlüsse ziehen:

• Die Expressionsrate von R steigt mit der Konzentration von A (Aktivierung)
• Die Expressionrate von A sinkt mit der Konzentration von R (Repression)

Wenn wir das System mathematisch beschreiben wollen, müssen Konstanten für Effekte auf beide Gene, sowie auf beiden Ebenen der Genexpression berücksichtigt werden (siehe Liste der Variablen und Konstanten). Wir gehen davon aus, dass eine genügend grosse Menge an Protein vorliegt, dass die Annahme von konstanter Lebensdauer eines Proteins gerechtfertigt ist. Aus demselben Grund nehmen wir an, dass die Translationsrate pro mRNA für beide Proteine konstant ist.

4.2 – Liste der Variablen und Konstanten

Symbol	Bedeutung	Beschreibung	variabel/ konstant
[latex]P[/latex]	Promotor im jeweiligen Zustand	Promotoren können besetzt oder frei vorliegen. Der Aktivierungszustand des gebundenen Promotors ist abhängig vom jeweiligen Gen. PR ist frei aktiv, PA ist im Komplex gebunden aktiv.	konstant
[latex]R(t)[/latex]	Konzentration des Proteins R (normalisiert)	Gibt an, wie viel Protein in Abhängigkeit der Zeit im System vorhanden ist.	variabel
[latex]A(t)[/latex]	Konzentration des Proteins A (normalisiert)
[latex]K_A[/latex]	Gleichgewichtskonstante der Reaktion [latex]P_{R, frei}+A\rightarrow P_{R, aktiv}[/latex]	Gibt an, wie stark die Bindung des Proteins an den entsprechenden Promotor ist.	konstant
[latex]K_R[/latex]	Gleichgewichtskonstante der Reaktion [latex]P_{A, aktiv}+R\rightarrow P_{A, besetzt}[/latex]
[latex]\tau_R[/latex]	Lebensdauer des Proteins [latex]R[/latex]	Gibt an, wie schnell das Protein im System abgebaut wird.	konstant
[latex]\tau_A[/latex]	Lebensdauer des Proteins [latex]A[/latex]
[latex]\beta[/latex]	Transkriptionswahrscheinlichkeit bei aktiviertem Promotor	Wahrscheinlichkeit, mit der ein Gen bei aktivem Promotor tatsächlich transkribiert wird.	konstant
[latex]m[/latex]	Translationsrate pro mRNA	Anzahl der Proteinmoleküle, die durch einen mRNA-Strang hergestellt werden können.	konstant

4.3 – Mathematische Grundlagen

Das mathematische Modell wird uns wiederholt zu einer inhomogenen linearen Differentialgleichung 1. Ordnung mit konstanten Koeffizienten (DGL) führen. Wir möchten hier kurz die wesentlichen Merkmale einer solchen DGL beschreiben und die unterschiedlichen Formen von Lösungsfunktionen angeben.

Definition

Eine solche DGL ist eine Gleichung der Form [latex]f^\prime = af + b[/latex] mit Zahlen [latex]a, b[/latex].
Eine Lösung einer DGL ist eine Funktion [latex]f[/latex], die wir in die DGL einsetzen und dann für alle [latex]t[/latex] gilt:

• Links steht die Zahl [latex]f'(t) =[/latex] der Wert der Ableitungsfunktion [latex]f'[/latex] zur Zeit [latex]t[/latex]
• Rechts steht die Zahl [latex]a f(t) +b =[/latex] der Wert, den wir erhalten, wenn wir den Funktionswert [latex]f(t)[/latex] zur Zeit [latex]t[/latex] einsetzen.

Der Graph einer Lösung heisst auch Lösungskurve. In jedem Punkt [latex](t_0,f(t_0))[/latex] auf diesem Graphen hat die Tangente dort eine Steigung [latex]f'(t_0)[/latex]. Da die Funktion die DGL erfüllt, ist dieser Wert gerade die rechte Seite [latex]a f(t_0) +b[/latex] für [latex]t =t_0[/latex].

Stationäre Lösungen

Besondere Lösungen sind stationäre Lösungen [latex]f_{\infty}[/latex] (auch Gleichgewichtslösung oder Fixpunkt genannt).
Für diese gilt [latex]f'_{\infty} = 0[/latex], also ist [latex]f =f_{\infty}[/latex] konstant.

Für [latex]a\neq 0[/latex] können wir die einzige stationäre Lösung hier angeben: \[\displaystyle f’_{\infty} = 0 = a f_{\infty} +b \implies f_{\infty}= – \frac ba.\]

Homogene Lösung

Sei [latex]f[/latex] eine beliebige Lösung mit [latex]f^\prime = af + b[/latex]. Wie beim Integrieren ist diese nicht eindeutig. Sie hängt von einer Konstante [latex]C[/latex] ab.

Sei zum Beispiel [latex]a = 0[/latex]. Dann ist eine Funktion [latex]f[/latex] gesucht mit [latex]f'(t) = b[/latex], also [latex]\displaystyle f(t) = \int b \; dt = b \cdot t + C.[/latex]

Was ist, wenn [latex]b = 0[/latex]? Dann heisst die DGL [latex]f^\prime = af[/latex]  homogen, und wir haben alle Lösungen der homogenen Differentialgleichung durch [latex]f_{H}(t) = C \cdot e^{at}.[/latex] Das lässt sich mit der Kettenregel und der Eigenschaft [latex](e^t)^\prime =e^t[/latex] direkt überprüfen. Zudem folgt, dass diese Lösung [latex]f_{H}(t) = C \cdot e^{at}[/latex] sogar eindeutig ist. Jede andere Funktion [latex]g[/latex], die [latex]g^\prime = ag[/latex] erfüllt, muss von dieser Form [latex]g(t) = C \cdot e^{at}[/latex] sein.

Allgemeine Lösung

Die Bestimmung von Lösungen einer beliebigen Differentialgleichung ist ein umfangreiches Gebiet der Mathematik. Hier werden Fragen untersucht, wie zum Beispiel: Gibt es überhaupt eine Lösung, kann ich diese explizit angeben, ist diese eindeutig, wie kann ich eine Lösung numerisch approximieren etc. ?

Hier bei den inhomogenen linearen Differentialgleichung 1. Ordnung mit konstanten Koeffizienten (DGL) lassen sich sämtliche Lösungen angeben. Jede Lösung von [latex]f^\prime = af + b[/latex] ist von der Form  [latex]\displaystyle f(t) =C \cdot e^{at} - \frac ba[/latex]. Daher heisst diese auch allgemeine Lösung.

Wir bemerken, dass die allgemeine Lösung der inhomogen DGL die Summe der allgemeinen Lösung der homogenen Differentialgleichung [latex]f^\prime = af[/latex]  und der stationären Lösung ist \[\displaystyle f(t) = f_{H}(t) + f_{\infty}(t) =C \cdot e^{at} – \frac ba.\]

Auch dies lässt sich direkt durch elementare Rechnungen mit den Ableitungsregeln überprüfen:

Rechne links los

\[ f'(t) = \left(C \cdot e^{at} – \frac ba\right)^\prime = a \cdot C \cdot e^{at} = a \left(\underbrace{C \cdot e^{at} – \frac ba}_{=f(t)} + \frac ba\right)  = a \left(f(t) + \frac ba\right) =a f(t) +  b \]

Anfangswert

In der allgemeinen Lösung [latex]\displaystyle f(t) =C \cdot e^{at} - \frac ba[/latex] haben wir eine Unbestimmtheit durch die Konstante [latex]C[/latex]. Wir erhalten also zunächst nur eine Schar von Lösungen. Geben wir einen Startwert [latex]f(t_0) = f_{0}[/latex] vor, wird die Lösung  eindeutig, und es gilt:

1. Zwei Lösungskurven zu unterschiedlichen Startwerten schneiden sich nicht.
2. Eine stationäre Lösung wird damit also nicht über- oder unterschritten.

Mit dem Anfangswert [latex]f(0) = f_{0}[/latex] berechnen wir die Konstante [latex]C[/latex] oben mit \[f(0) = N_{0} = C\cdot e^{0} – \frac ba = C – \frac ba \implies C = f_{0} + \frac ba.\] Setzen wir dieses [latex]C[/latex] ein, erhalten wir \[f(t) = \left(f_{0} + \frac ba \right) \cdot e^{at} – \frac ba = f_{0} \cdot e^{at} + \frac ba \left (e^{at} -1 \right).\]

Konvergenz

Für die qualitative Analyse des Lösungsverhalten einer DGL hilft der Ansatz, über das Konvergenzverhalten einer Lösung Informationen zu gewinnen. In der Biologie würde das bedeuten, ob die Proteinkonzentrationen sich nach einer gewissen Zeit einem Grenzwert nähern.

Ist der Startwert [latex]f(0) = f_{0} = f_\infty[/latex] gleich der stationären Lösung, so bleibt die Entwicklung [latex]f(t)[/latex] konstant, da dann [latex]f'_\infty = 0[/latex].

Was passiert, wenn wir ein wenig von der stationären Lösung weggehen?

Gilt dann [latex]f(t) \to f_\infty[/latex]? Oder werden sich die Funktionswerte [latex]f(t)[/latex] von dem Wert [latex]f_\infty[/latex] entfernen?

Für das Beispiel [latex]f^\prime = af + b[/latex] mit der Lösung [latex]\displaystyle f(t)=C\cdot e^{at}-\frac{b}{a}[/latex] lässt sich dies direkt beantworten, wenn wir den Lösungsfunktionsausdruck [latex]f(t)[/latex] anschauen:

Im Fall [latex]a > 0[/latex] gilt [latex]e^{at} \to \infty[/latex]  für [latex]t \to \infty[/latex].

Im Fall [latex]a 0[/latex] .

Unterscheiden wir noch, ob der Startwert über [latex]f(0) > f_\infty[/latex] oder [latex]f(0)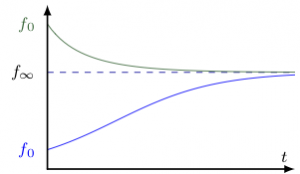

Lösungen der Differenzialgleichung [latex]f'=af+b [/latex] mit unterschiedlichen Startwerten [latex] f_0 [/latex]. In jedem Fall konvergiert die Lösungskurve gegen die Gleichgewichtslösung [latex]f_\infty [/latex].

Das Monotonieverhalten der Lösung ist durch die erste Ableitung, also linke Seite von [latex]f^\prime = af + b[/latex] bestimmt. Die rechte Seite ist eine fallende Gerade (da [latex]a f_\infty[/latex] so ist [latex]f'(0) = af(0) + b