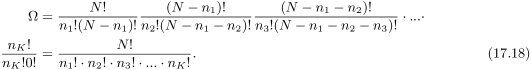¹Ausführliche Herleitung: Die Aufgabe lässt sich auch so formulieren: Angenommen wir haben [katex]N[/katex] Teilchen, wie viele Möglichkeiten gibt es diese auf [katex]K[/katex] Boxen zu verteilen, wobei [katex]n_1[/katex] Teilchen in die Box 1, [katex]n_2[/katex] Teilchen in die Box 2, [katex]n_3[/katex] Teilchen in die Box 3, ..., [katex]n_K[/katex] Teilchen in die Box [katex]K[/katex] kommen. Zu Beginn ziehen wir also [katex]n_1[/katex] Teilchen und legen sie in Box 1. Auf wie viele Arten ist dies möglich? Falls [katex]n_1 = 1[/katex] ist, so gibt es [katex]N[/katex] Möglichkeiten. Falls [katex]n_1 = 2[/katex] ist, so gibt es [katex]N[/katex] Möglichkeiten für die Auswahl des ersten Teilchens und [katex]N - 1[/katex] Möglichkeiten das zweite Teilchen auszuwählen. Zusätzlich spielt es keine Rolle, welches der beiden Teilchen zuerst gezogen wird. Folglich gibt es [katex]N(N-1)/2! = N!/(2!(N - 2)!)[/katex] Möglichkeiten 2 Teilchen aus [katex]N[/katex] Teilchen auszuwählen. Falls nun [katex]n_1[/katex] beliebig ist, gibt es entsprechend [katex]N!/(n_1!(N - n_1)!)[/katex] Möglichkeiten [katex]n_1[/katex] Teilchen aus [katex]N[/katex] Teilchen auszuwählen. In einem nächsten Schritt geht es jetzt darum aus den restlichen [katex]N - n_1[/katex] Teilchen [katex]n_2[/katex] Teilchen auszuwählen. Analog gilt für die Anzahl Möglichkeiten dies zu tun [katex](N - n_1)!/(n_2!(N - n_1 - n_2)!)[/katex]. Führt man diese Auswahl der Teilchen weiter bis alle [katex]N[/katex] Teilchen auf die [katex]K[/katex] Boxen verteilt sind, ergibt sich für die Anzahl Mikrozustände [katex]\Omega [/katex] zu einem gegebenen Makrozustand