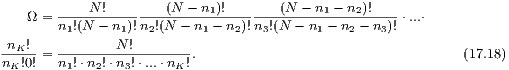1Ausführliche Herleitung: Die Aufgabe lässt sich auch so formulieren: Angenommen wir
haben 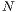 Teilchen, wie viele Möglichkeiten gibt es diese auf
Teilchen, wie viele Möglichkeiten gibt es diese auf 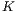 Boxen zu verteilen,
wobei
Boxen zu verteilen,
wobei 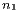 Teilchen in die Box 1,
Teilchen in die Box 1, 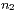 Teilchen in die Box 2,
Teilchen in die Box 2, 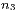 Teilchen in die
Box 3, ...,
Teilchen in die
Box 3, ..., 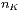 Teilchen in die Box
Teilchen in die Box 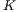 kommen. Zu Beginn ziehen wir also
kommen. Zu Beginn ziehen wir also 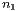 Teilchen und legen sie in Box 1. Auf wie viele Arten ist dies möglich? Falls
Teilchen und legen sie in Box 1. Auf wie viele Arten ist dies möglich? Falls 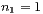 ist,
so gibt es
ist,
so gibt es 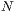 Möglichkeiten. Falls
Möglichkeiten. Falls 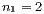 ist, so gibt es
ist, so gibt es 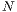 Möglichkeiten für
die Auswahl des ersten Teilchens und
Möglichkeiten für
die Auswahl des ersten Teilchens und 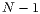 Möglichkeiten das zweite Teilchen
auszuwählen. Zusätzlich spielt es keine Rolle, welches der beiden Teilchen zuerst
gezogen wird. Folglich gibt es
Möglichkeiten das zweite Teilchen
auszuwählen. Zusätzlich spielt es keine Rolle, welches der beiden Teilchen zuerst
gezogen wird. Folglich gibt es 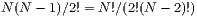 Möglichkeiten 2
Teilchen aus
Möglichkeiten 2
Teilchen aus 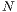 Teilchen auszuwählen. Falls nun
Teilchen auszuwählen. Falls nun 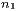 beliebig ist, gibt es entsprechend
beliebig ist, gibt es entsprechend
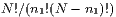 Möglichkeiten
Möglichkeiten 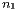 Teilchen aus
Teilchen aus 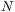 Teilchen auszuwählen. In
einem nächsten Schritt geht es jetzt darum aus den restlichen
Teilchen auszuwählen. In
einem nächsten Schritt geht es jetzt darum aus den restlichen 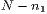 Teilchen
Teilchen
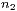 Teilchen auszuwählen. Analog gilt für die Anzahl Möglichkeiten dies zu tun
Teilchen auszuwählen. Analog gilt für die Anzahl Möglichkeiten dies zu tun
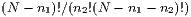 . Führt man diese Auswahl der Teilchen weiter bis alle
. Führt man diese Auswahl der Teilchen weiter bis alle 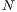 Teilchen auf die
Teilchen auf die 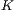 Boxen verteilt sind, ergibt sich für die Anzahl Mikrozustände
Boxen verteilt sind, ergibt sich für die Anzahl Mikrozustände 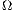 zu einem
gegebenen Makrozustand
zu einem
gegebenen Makrozustand