12.1 – Parameter
Ein oder auch eine Formvariable ist eine an sich unabhängige Variable. Parameter – (deutsch) auch Übergabewerte genannt – sind in der Informatik Variablen, durch die ein Computerprogramm auf die Verarbeitung bestimmter Werte „eingestellt“ werden kann. Parameter sind also programmextern gesetzte Einflussfaktoren. Durch Parametrisierung können Programme in ihrer Anwendung flexibilisiert werden, ohne dass das Programm dazu neu erstellt werden muss. Welche Werte eingestellt werden können, muss bei der Erstellung von Programmen festgelegt werden.
12.2 – Parametrisches Design
Parametrisches Design ist eine Designmethode, bei der Merkmale (wie Gebäudeelemente und technische Komponenten) nach algorithmischen Prozessen geformt werden, anstatt direkt modelliert zu werden. Als Parameter definiert werden können dabei einfache Grössen wie Längen, Breiten und Höhen von Beuteilen, Grenzwerte, Winkel, oder andere Abhängigkeiten. Bei dieser Methode bestimmen Parameter und Regeln die Beziehung zwischen Designabsicht und Designantwort. Der Begriff parametrisch bezieht sich auf Eingabeparameter, die in die Algorithmen eingespeist werden.
Das Potential von parametrischem Design ist vielfältig:
- Fehler vermeiden (präzises, numerisches Modellieren)
- Schnelles Anpassen von Design
- Modellieren von komplexer Geometrie
- Generieren von individualisierten Elementen
- Generieren von Design-variationen
- Generieren von Familien von Elementen
- Generieren von Exportdaten z.B. zur Fabrikation
Gebäude können von der ersten Entwurfsphase an auf ein Optimum ( z. B. Zeit, Kosten, Qualität) in der Planung, Vorfertigung, Ausführung und Nutzung hin konzipiert werden. Parametrische Planung ist bei komplexen Projekten mit vielen Akteuren besonders sinnvoll, da Änderungen im Planungsverlauf problemlos in das parametrische Modell eingearbeitet werden können. Verschiedene Entwurfsvarianten erleichtern somit grundlegende Entscheidungen in der Anfangsphase von Planungen. Die durchgängige Parametrisierung eines einzelnen Produkts bzw. Bauteils inklusive seines „Zubehörs“ (Formwerkzeuge, Fertigungsverfahren, Materialeigenschaften etc.) stellt eine geschlossene digitale Prozesskette sicher.
Parametrismus ist ein Stil innerhalb der zeitgenössischen Avantgarde-Architektur, der als Nachfolger der modernen und postmodernen Architektur gefördert wird. Der Begriff wurde 2008 von Patrik Schumacher, einem Architekturpartner von Zaha Hadid (1950–2016), geprägt. Parametrismus hat seinen Ursprung im parametrischen Design, das auf den Einschränkungen in einer parametrischen Gleichung basiert. Parametrismus stützt sich auf Programme, Algorithmen und Computer, um Gleichungen für Designzwecke zu manipulieren.
Aspekte des Parametrismus wurden in Stadtplanung, Architekturdesign, Innenarchitektur und Möbeldesign verwendet. Befürworter des Parametrismus haben erklärt, dass eines der bestimmenden Merkmale darin besteht, dass „Parametrismus impliziert, dass alle Elemente des Designs parametrisch variabel und wechselseitig anpassungsfähig werden.“ Laut Schumacher ist Parametrismus eine Autopoiesis oder ein selbstreferenzielles System bei dem alle Elemente miteinander verbunden sind und ein äußerer Einfluss, der eines verändert, alle anderen verändert.
12.3 – Mapping
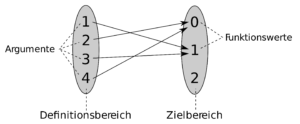
Ein zentrales Konzept der Mathematik ist die Abbildung, die auch Funktion genannt wird (engl. Mapping). Abbildungen sind eindeutige Zuordnungen zwischen zwei Mengen A und B. Dies bedeutet, dass jedem Element durch die Abbildung genau ein Element zugeordnet wird. Ein Beispiel hierfür ist die Quadratfunktion von der Menge in die Menge , die jeder reellen Zahl ihre Quadratzahl zuordnet. Die Schreibweise für Abbildungen von nach ist:
Ausgesprochen wird dieser Ausdruck so:
Hinweis
Die Begriffe „Abbildung“ und „Funktion“ sind beide in der Mathematik üblich und bedeuten genau dasselbe.
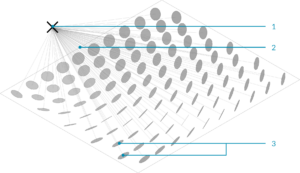
- Attraktor Punkt, 2.:Vektoren, 3: Kreise zu dem Attraktor orientiert, basierend auf deren Normalen. In diesem Beispiel wird die Orientierung zum Attraktor auf die Rotation der Kreise abgebildet.
- Verschiedene Positionen des Attraktors
- Höhenfeld (Heightmap)
- Mesh, deformiert durch Höhenfeld (Heightmap)
- Lochgrösse und Extrusionstiefe, De Young Museum.
- De Young Museum, Herzog & DeMeuron
12.4 – Rekursion
Als Rekursion (lateinisch recurrere ‚zurücklaufen‘) wird ein prinzipiell unendlicher Vorgang, der sich selbst als Teil enthält oder mithilfe von sich selbst definierbar ist, bezeichnet. Üblicherweise sind rekursive Vorgänge relativ kurz beschreibbar bzw. können durch eine relativ kurze Anweisung ausgelöst werden. Die bei Rekursion aufeinander folgenden Teilvorgänge oder die nacheinander erzeugten Objekte sind nicht unabhängig voneinander, sondern zwischen jedem Schrittpaar oder Objektpaar besteht eine besondere, die rekursive Beziehung. (Quelle)
12.5 – Fraktal
Fraktal ist ein vom Mathematiker Benoît Mandelbrot 1975 geprägter Begriff (lateinisch fractus ‚gebrochen‘, von lateinisch frangere‚ (in Stücke zer-)‚brechen‘), der bestimmte natürliche oder künstliche Gebilde oder geometrische Muster bezeichnet. Gebilde weisen eine hohen Grad von Skaleninvarianz bzw. Selbstähnlichkeit auf. Das ist beispielsweise der Fall, wenn ein Objekt aus mehreren verkleinerten Kopien seiner selbst besteht. Geometrische Objekte dieser Art unterscheiden sich in wesentlichen Aspekten von gewöhnlichen glatten Figuren. (Quelle)

Abbildung 12.13 – Mandelbrot Menge
Abbildung 12.14 – Börsendaten im Zeitraum von 6 Monaten
Abbildung 12.15 – Börsendaten im Zeitraum von 6 Stunden
12.6 – L-System
Bei den Lindenmayer- oder L-Systemen handelt es sich um einen mathematischen Formalismus, der 1968 von dem ungarischen theoretischen Biologen Aristid Lindenmayer als Grundlage einer axiomatischen Theorie biologischer Entwicklung vorgeschlagen wurde. In jüngerer Zeit fanden L-Systeme Anwendung in der Computergrafik bei der Erzeugung von Fraktalen und in der realitätsnahen Modellierung von Pflanzen.
Das wesentliche Prinzip von L-Systemen besteht in der sukzessiven Ersetzung von Einzelteilen eines einfachen Objektes mittels sogenannter Produktionsregeln. Diese Ersetzungen können rekursiv durchgeführt werden. Damit gehören L-Systeme zu den sogenannten Ersetzungssystemen. (Quelle)

Abbildung 12.16 – Fraktale Bäume, mit einem L-System generiert.
12.7 – Shape Grammar
Shape grammars, deutsch Formen-Grammatiken, sind eine Art von Produktionssystem in der Informatik zur Generierung von geometrischen Formen. Üblicherweise werden Shape grammars zur Erzeugung von zwei- bzw. dreidimensionalen Formen eingesetzt, heutzutage vor allem in den Bereichen der Architektur und Computergrafik. Die Grundlage für Shape grammars wurde in einem Seminar-Artikel von George Stiny und James Gips im Jahr 1971 geschaffen.[1]
Eine Shape grammar besteht aus Regeln sowie einer Generierungs-Engine, welche die Regeln auswählt und verarbeitet bzw. berechnet. Eine Regel definiert wie eine existierende Figur (bzw. ein Teil davon) im Geometrischen Raum transformiert werden kann. Die Definition einer Shape grammar folgt der Standarddefinition einer Phrasenstrukturgrammatik von Chomsky, wobei statt Symbolen, Figuren („shapes“) verwendet werden.
Eine Shape grammar generiert eine Form durch rekursives Anwenden der Shape rules, beginnend mit der Startfigur. Das Ergebnis der angewendeten Regel auf eine vorhandene Form, ist immer eine neue Form, die aus der vorhandenen Form besteht, wobei ein Vorkommnis der linken Seite der Regel in der neuen Form durch die Form auf der rechten Seite der Regel ersetzt wurde.
Eine Shape grammar besteht minimal aus drei Produktionsregeln (=Shape rules). Einer Anfangsregel, zumindest einer Transformationsregel und einer Terminierungsregel. Die Startregel ist erforderlich um den Generierungsprozess zu starten, während die Terminierungsregel notwendig ist um die Generierung abzuschließen. Der einfachste Weg den Prozess zu stoppen, ist es den Marker (=Nonterminale) zu entfernen. Im Gegensatz zu Chomsky-Grammatiken können Produktionsregeln in Shape grammars nicht nur seriell, sondern auch parallel angewendet werden, ähnlich dem Ablauf von L-Systemen.
Shape grammars wurden ursprünglich für Gemälde und Skulpturen präsentiert,[1] haben seither jedoch vor allem in der theoretischen und akademischen Architektur (Computer-aided architectural design) Anwendung gefunden. Shape grammars eignen sich dabei vor allem für kleine, klar definierte Probleme, wie etwa Struktur und Layout von Innenräumen oder Fassaden von Gebäuden. Shape grammars bestehen dabei sehr oft aus einer großen Anzahl an Regeln. So besteht die von William Mitchell[2] präsentierte Shape grammar zur Generierung einer Villa im Stile des italienischen Architekten Andrea Palladio aus 69 Regeln, die in acht Durchführungsschritten angewendet werden.
Ähnlich zur Anwendung in der Architektur haben Shape grammars auch in der Computergrafik in den letzten Jahrzehnten an Bedeutung gewonnen. Shape grammars werden dabei vor allem bei der prozeduralen Modellierung von Gebäuden oder Städten eingesetzt (z. B.: für Filme oder Videospiele). Shape Grammars bilden dabei die Grundlage für zahlreiche entwickelter Systeme die anhand von Produktionsregeln eine Variation von unterschiedlichen 3D-Modellen generieren. Sowohl realistisch aussehende Straßenplänen, als auch Fassaden oder Innenräume von Gebäuden können dabei mit Hilfe von Shape Grammars prozedural erstellt werden.[3][4][5] Zu weiteren Bereichen in denen Shape grammars angewendet wurden, zählen Industriedesign und Ingenieurswissenschaften. (Quelle)
12.8 – Bildtafeln
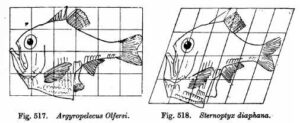
- Thompson illustrierte die Transformation von Argyropelecus olfersi in Sternoptyx diaphana durch die Anwendung einer 20° Scherungs-abbildung (engl. shear mapping).
- Die Orientierung von Attraktoren auf verschiedene geometrische Transformationen abgebildet
- ASCII Zeichen nach Helligkeitswerten abgebildet
- Sinusfunktionen werden auf die Deformierung einer Mesh-fläche abgebildet
- Greg Lynn – Embryonic House
- Nervous Systems
- 3D-gedruckte parametrische Schuhsohle
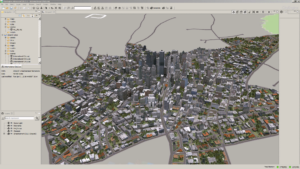
- City Engine
City-Engine: Procedural City Generator basierend auf Prinzipien von Shape Grammar
Ein Parameter oder auch eine Formvariable ist eine an sich unabhängige Variable, die aber zumindest in einer gegebenen Situation eher als eine festgehaltene Größe aufgefasst wird.
 durch die Abbildung
durch die Abbildung  genau ein Element
genau ein Element  zugeordnet wird. Ein Beispiel hierfür ist die Quadratfunktion von der Menge
zugeordnet wird. Ein Beispiel hierfür ist die Quadratfunktion von der Menge  in die Menge
in die Menge  ihre Quadratzahl
ihre Quadratzahl  zuordnet. Die Schreibweise für Abbildungen von
zuordnet. Die Schreibweise für Abbildungen von  nach
nach  ist:
ist: