14.1 – Entwerfen als Variantenerzeugung und Einschränkung

14.2 – Probleme

Gemeinsam mit Melvin Webber prägte Horst Rittel ab Mitte der 1960er Jahre den Begriff „Wicked Problems“. Der im deutschen bisweilen als „bösartige Probleme“ übersetzte Begriff zielt auf die große Bandbreite undefinierter Probleme, die sich beispielsweise in Planungs- oder Gestaltungsprozessen ergeben. Horst Rittel, der als einer der ersten eine Theorie der wicked problems formuliert hat, nennt zehn Merkmale^[2] dieser komplexen Sachverhalte:

1. Wicked problems haben keine definitive Formulierung. Das Problem der Armut in Texas ist dem Problem der Armut in Nairobi zwar ähnlich, unterscheidet sich aber dennoch von dem in Nairobi, so dass keine praktischen Merkmale “Armut” beschreiben.
2. Es ist schwer, vielleicht sogar unmöglich, den Erfolg von wicked problems zu messen oder zu beanspruchen, weil sie ineinander fließen, einander bedingen, im Gegensatz zu den Grenzen traditioneller Gestaltungsprobleme, die vergleichsweise klar artikuliert oder definiert werden können.
3. Lösungen für wicked problems können nur gut oder schlecht, nicht wahr oder falsch sein. Es gibt keinen idealisierten Endzustand, den es zu erreichen gilt, und deshalb sollten Ansätze für wicked problems tragfähige Wege sein, um eine Situation zu verbessern, anstatt sie zu lösen.
4. Es gibt keine Schablone, an die man sich halten kann, wenn man ein wicked problem angeht, wenngleich die Geschichte als Leitfaden dienen kann. Teams, die sich mit wicked problems auseinandersetzen, müssen buchstäblich Dinge erfinden, während sie voranschreiten.
5. Es gibt immer mehr als eine Erklärung für ein wicked problem, wobei die Angemessenheit der Erklärung stark von der individuellen Perspektive des/r Gestaltenden abhängt.
6. Jedes wicked problem ist ein Symptom für ein anderes Problem. Die vernetzte Qualität sozioökonomischer politischer Systeme veranschaulicht, wie z.B. eine Veränderung in der Bildung zu einem neuen Ernährungsverhalten führt.
7. Keine Abmilderungsstrategie für ein wicked problem verfügt über einen definitiven wissenschaftlichen Test, weil wicked Problems mit Menschen zu tun haben und die (Natur-) Wissenschaft insbesondere darauf ausgerichtet ist, natürliche Phänomene zu verstehen.
8. Das Anbieten einer “Lösung” für ein wicked problem ist häufig ein “One-Shot”, weil eine signifikante Intervention den Gestaltungsraum so weit verändert, dass die Fähigkeit zum Ausprobieren minimiert wird.
9. Jedes wicked problem ist einzigartig.
10. Konstrukteure, die versuchen, ein wicked problem zu lösen, müssen die volle Verantwortung für ihre Handlungen übernehmen.

(Quelle)

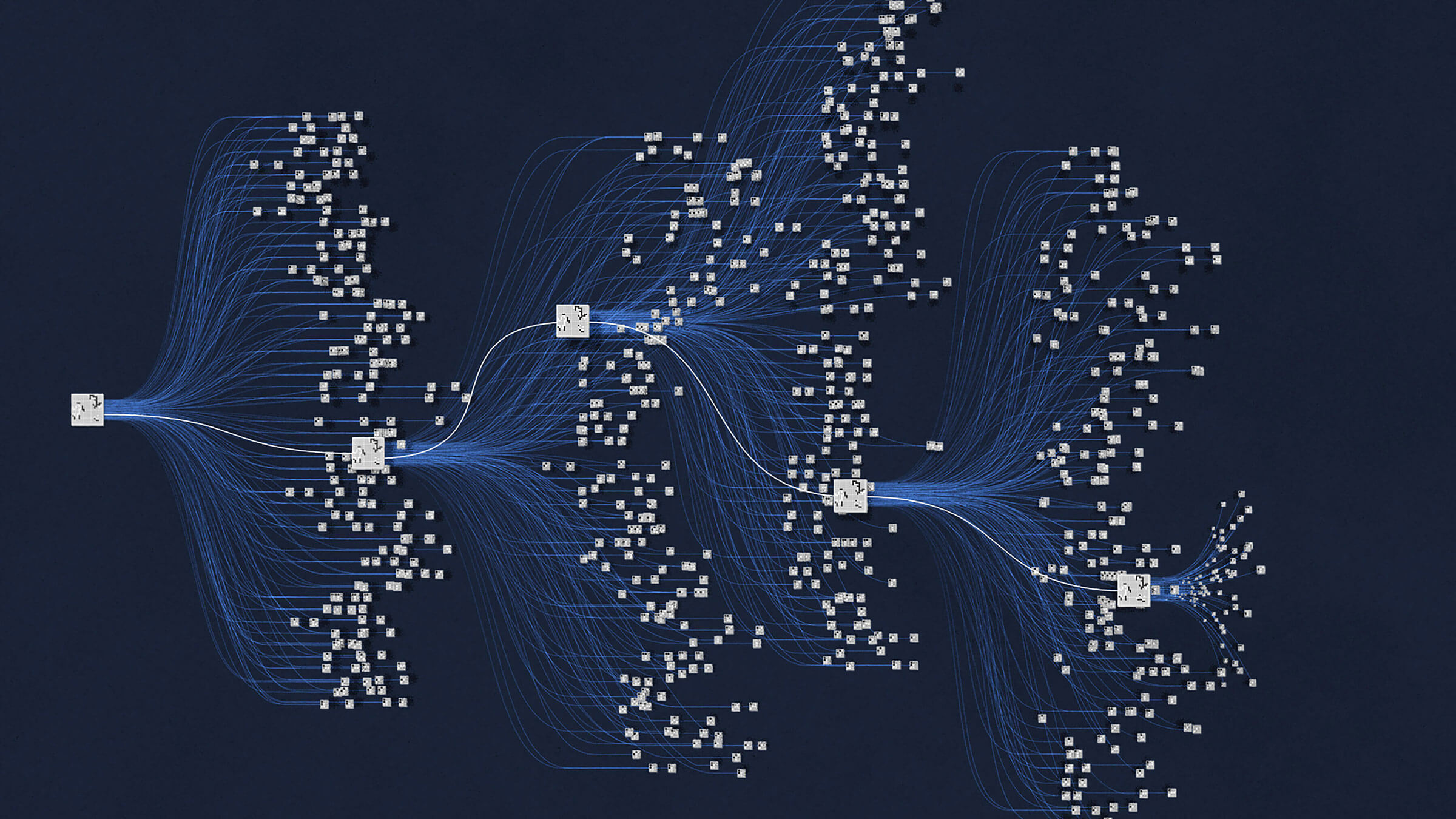
Abbildung 14.1 – Ausschnitt aus dem Entscheidungsbaum des Spiels GO

14.3 – Heuristik

Heuristik (von altgriechisch εὑρίσκω heurísko (ich finde); von εὑρίσκειν heurískein (auffinden entdecken)) bezeichnet die Kunst, mit begrenztem Wissen (unvollständigen Informationen) und wenig Zeit dennoch zu wahrscheinlichen Aussagen oder praktikablen Lösungen zu kommen. Es bezeichnet ein analytisches Vorgehen, bei dem mit begrenztem Wissen über ein System mit Hilfe mutmaßender Schlussfolgerungen Aussagen über das System getroffen werden. Die damit gefolgerten Aussagen weichen oftmals von der optimalen Lösung ab. Durch Vergleich mit einer optimalen Lösung kann die Güte der Heuristik bestimmt werden.

Bekannte Heuristiken sind zum Beispiel Versuch und Irrtum (trial and error), statistische Auswertung von Zufallsstichproben und das Ausschlussverfahren. Heuristische Verfahren basieren auf Erfahrungen; sie können auch auf „falschen“ Erfahrungen (z. B. verzerrte Wahrnehmung, Scheinkorrelation) basieren. (Quelle)

14.4 – Evolutionäre Algorithmen

Evolutionäre Algorithmen (EA) sind eine Klasse von stochastischen, metaheuristischen Optimierungsverfahren, deren Funktionsweise von der Evolution natürlicher Lebewesen inspiriert ist.

In Anlehnung an die Natur werden Lösungskandidaten für ein bestimmtes Problem künstlich evolviert, EA sind also naturanaloge Optimierungsverfahren. Die Zuordnung zu den stochastischen und metaheuristischen Algorithmen bedeutet vor allem, dass EA meist nicht die beste Lösung für ein Problem finden, aber bei Erfolg eine hinreichend gute, was in der Praxis vor allem bei NP-vollständigen Problemen bereits wünschenswert ist. Die Verfahren verschiedener EA unterscheiden sich untereinander in erster Linie durch die genutzten Selektions-, Rekombinations– und Mutationsoperatoren, das Genotyp–Phänotyp-Mapping sowie die Problemrepräsentation.

Die ersten praktischen Implementierungen evolutionärer Algorithmen wurden Ende der 1950er Jahre veröffentlicht,^[2] allerdings äußerten sich bereits in den vorhergehenden Jahrzehnten Wissenschaftler zum Potenzial der Evolution für maschinelles Lernen.

Die Anwendungen von EA gehen über Optimierung und Suche hinaus und finden sich auch in Kunst, Modellierung und Simulation, insbesondere auch bei der Untersuchung evolutionsbiologischer Fragestellungen.

Das grobe Verfahren evolutionärer Algorithmen besteht meist aus einer Initialisierung und einer Generationsschleife, die solange durchlaufen wird, bis ein Abbruchkriterium erfüllt ist:

1. Initialisierung: Die erste Generation von Lösungskandidaten wird (meist zufällig) erzeugt.
2. Evaluation: Jedem Lösungskandidaten der Generation wird entsprechend seiner Güte ein Wert der Fitnessfunktion zugewiesen.
3. Durchlaufe die folgenden Schritte, bis ein Abbruchkriterium erfüllt ist:
   1. Selektion: Auswahl von Individuen meist basierend auf ihrer Fitness, die die Eltern für die Rekombination bilden
   2. Rekombination: Erzeugung von Nachkommen durch zufällige Kombination der Genome der Eltern
   3. Mutation: Zufällige Veränderung aller oder eines Teils der Nachkommen
   4. Evaluation: Jedem Nachkommen wird entsprechend seiner Güte ein Wert der Fitnessfunktion zugewiesen.
   5. Selektion: Bestimmung einer neuen Generation aus der alten und/oder den in dieser Generation gebildeten Nachkommen

(Quelle)

14.5 – Fitnesslandschaft

Eine Fitnessfunktion ist die Zielfunktion eines evolutionären (Optimierungs-)Algorithmus (EA). Gelegentlich wird eine Fitnessfunktion auch als Teil einer Zielfunktion beschrieben oder umgekehrt. Wie auch evolutionäre Algorithmen haben Fitnessfunktionen ein biologisches Vorbild, die biologische Fitness, die den Grad der Anpassung eines Organismus an seine Umgebung angibt und einen wesentlichen Faktor für seine Reproduktionswahrscheinlichkeit darstellt. Bei evolutionären Algorithmen beschreibt die Fitness eines Lösungskandidaten, wie gut er das zugrunde liegende Optimierungsproblem löst. Die Fitnessfunktion berechnet aus den Eigenschaften eines Lösungsversuchs, wie gut sich dieses „Individuum“ bzgl. des gestellten Problems als Lösung eignet.

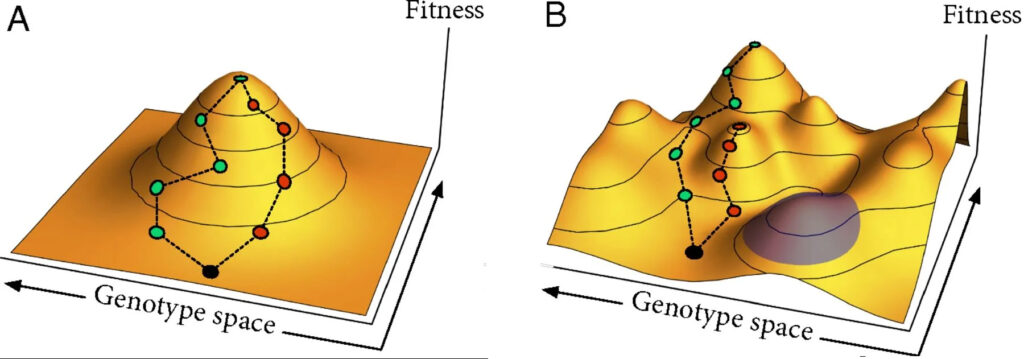
Abbildung 14.2 – Fitnesslandschaft

Eine Fitnessfunktion muss nicht zwangsläufig einen absoluten Wert berechnen können, da es oft reicht, Kandidaten zu vergleichen, um den besseren auszuwählen. Eine relative Angabe der Fitness (Kandidat a ist besser als b) genügt in manchen Fällen, wie z. B. bei der der Pareto-Optimierung. Ein Pareto-Optimum (auch Pareto-effizienter Zustand) ist ein (bestmöglicher) Zustand, in dem es nicht möglich ist, eine (Ziel-)Eigenschaft zu verbessern, ohne zugleich eine andere verschlechtern zu müssen. (Quelle)

Abbildung 14.3 – y-Achse: Festigkeit x-Achse: „Leichtigkeit“ (=Kehrwert der Masse) Ein Bauteil soll sowohl belastbar als auch leicht werden. Es sei also gekennzeichnet durch die zwei Eigenschaften Festigkeit und Masse. Je höher die Festigkeit und je geringer die Masse, desto besser sei das Bauteil. Trägt man die Wertepaare für viele verschiedene Bauteile in ein Diagramm ein, das Festigkeit und Leichtigkeit (Kehrwert der Masse) gegenüberstellt, so erhält man die blau markierte Menge.