5.1 – NURBS
In den 1950er Jahren wurden besonders im Automobil- und Schiffbau für die fehlerfreie Reproduzierbarkeit technischer Bauteile mathematisch exakte Beschreibungen von Freiformflächen benötigt. Vor dieser Zeit wurden derartige Oberflächen durch einzelne von einem Konstrukteur hergestellte physikalische Modelle beschrieben. So begann unter anderem der Ingenieur Pierre Étienne Bézier, zu dieser Zeit bei Renault in Frankreich, mit der Entwicklung der nach ihm benannten Bézierkurve. Unabhängig von Bézier arbeitete Paul de Casteljau, angestellt bei Citroën, zur gleichen Zeit auch an diesem mathematischen Problem. Weil Bézier die Ergebnisse seiner Arbeit veröffentlichte, werden heutzutage in der graphischen Datenverarbeitung Splines, deren Kontrollpunkte nicht auf der Kurve selbst liegen, als „Bézier-Spline“ bezeichnet, während der Name von de Casteljau in dem nach ihm benannten Algorithmus fortlebt, der für die numerische Verarbeitung parametrischer Flächen eingesetzt wird. In den 1960er Jahren wurde klar, dass non-uniform rational B-Splines (NURBS) eine Generalisierung von Bézier-Splines sind. (Quelle)
NURBS-Kurven und -Flächen verhalten sich ähnlich und haben eine gemeinsame Terminologie. Da Kurven am einfachsten zu beschreiben sind, werden wir sie genauer betrachten. Eine NURBS-Kurve wird durch vier Dinge definiert: Grad, Kontrollpunkte, Knoten und Bewertungsregel.
5.2 – Kurven
NURBS-Kurven und -Flächen sind die vorrangigen mathematischen Darstellungen, die Nurbsbasierte CAD Software wie Rhino zur Geometriedarstellung verwendet. NURBS ist eine genaue mathematische Darstellung von Kurven, deren Bearbeitung sehr intuitiv geschieht. Freiformkurven können leicht unter Verwendung von NURBS dargestellt werden, und dank der Kontrollstruktur ist eine leichte und vorhersagbare Bearbeitung möglich.
5.2.1 – Kurvenparameter
Ein Parameter auf einer Kurve repräsentiert die Adresse eines Punkts auf dieser Kurve. Man kann sich die parametrische Kurve als einen innerhalb einer bestimmten Zeit zurückgelegten Weg zwischen zwei Punkten vorstellen, dies mit einer festgelegten oder variablen Geschwindigkeit. Wenn für die Wegstrecke der Zeitraum T benötigt wird, dann repräsentiert der Parameter t eine Zeit innerhalb von T, welche als ein Standort (Punkt) auf der Kurve erscheint.
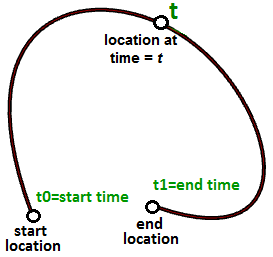
Abbildung 5.1 – Zeit ist der Parameter zur Bestimmung der Wegstrecke einer parametrischen Kurve . Der von Beginn bis Ende benötigte Zeitraum wird Kurvendomäne oder Intervall genannt.
5.2.2 – Kurvendomäne oder Intervall
Eine Kurvendomäne oder Intervall wird definiert als der Bereich von Parametern, die zu einem Punkt innerhalb dieser Kurve ausgewertet werden. Die Domäne wird gewöhnlich mit zwei reellen Zahlen beschrieben, welche die in der Form (min bis max) oder (min, max) ausgedrückten Domänenbeschränkungen definieren. Die Domänenbeschränkungen können zwei beliebige Werte sein, die auf die tatsächliche Länge der Kurve bezogen sein können oder auch nicht. In einer ansteigenden Domäne wird der Parameter der min-Domäne zum Startpunkt der Kurve ausgewertet, und max-Domäne zum Endpunkt der Kurve.
5.2.3 – Kurvenauswertung
Wir haben gelernt, dass es sich bei einem Kurvenintervall um den Bereich aller Parameterwerte handelt, die zu Punkten innerhalb der 3D-Kurve ausgewertet werden. Es besteht jedoch keinerlei Garantie, dass beispielsweise die Auswertung auf der Mitte der Domäne einen Punkt in der Mitte der Kurve ergibt.
Die gleichförmige Parametrisierung einer Kurve können wir uns vorstellen, als würden wir eine Wegstrecke mit konstanter Geschwindigkeit zurücklegen. Eine Linie von Grad 1 zwischen zwei Punkten wäre ein Beispiel, bei dem gleiche Intervalle von Parametern gleiche Intervalle einer Bogenlänge auf der Linie ergeben. In parametrischen Kurven werden gleiche Intervalle von Parametern nur selten zu gleichen Intervallen auf der 3D-Kurve ausgewertet.
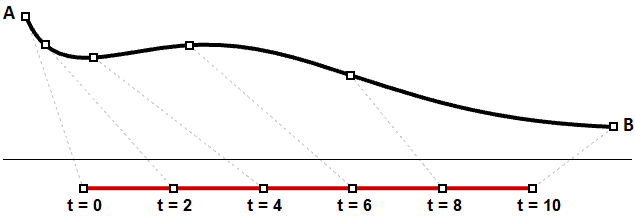
Abbildung 5.2 – Parameterspace (Domäne) von 0-10 einer Kurve. Gleiche Parameterintervalle ergeben typischerweise keine gleich langen Abstände auf einer parametrischen Kurven, etwa NURBS-Kurven.
5.2.4 – Kurvengrad
Der Kurvengrad ist eine ganze positive Zahl. Rhino ermöglicht das Arbeiten mit jeglicher Gradkurve, beginnend bei 1. Die Grade 1, 2, 3 und 5 sind die nützlichsten, Grad 4 und alle über Grad 5 hingegen finden in der wirklichen Welt wenig Anwendung. Manchmal werden die Begriffe linear (Grad 1), quadratisch (Grad 2), und kubisch verwendet (Grad 3). Es folgen einige Beispiele für Kurven und ihren Grad:
- Linien und Polylinien sind NURBS-Kurven ersten Grades (gerade Liniensegmente verbinden die Kontrollpunkte).
- Kreise und Ellipsen können mit NURBS auch beschrieben werden, erfordern jedoch eine besondere Gewichtung der Kontrollpunkte.
- Freiform-Kurven werden gewöhnlich als NURBS-Kurven dritten oder fünften Grades dargestellt.
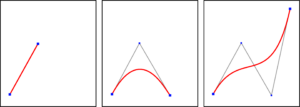
Abbildung 5.3 – Bézierkurven dritten Grades (rot) und die zugehörigen Kontrollpolygone (grau). Von links nach rechts wurde jeweils ein weiterer Kontrollpunkt (blau) hinzugefügt. Man erkennt, wie die Kurve bei Einfügen/Verändern eines Kontrollpunkts ihre Richtung und/oder Krümmung variiert.
Es ist möglich, den Grad einer NURBS-Kurve zu erhöhen, aber nicht ihre Form zu verändern. Es ist jedoch im Allgemeinen nicht möglich, den Grad einer NURBS-Kurve zu reduzieren, ohne ihre Form zu ändern.
5.2.5 – Kontrollpunkte
Die Kontrollpunkte einer NURBS-Kurve ist eine Liste von (Grad+1)-Punkten. Die intuitivste Methode, die Form einer NURBS-Kurve zu verändern, besteht in der Verschiebung ihrer Kontrollpunkte.
Die Anzahl der Kontrollpunkte, die sich auf das jeweilige Segment einer NURBS- Kurve auswirken, wird durch den Kurvengrad bestimmt. Beispielsweise unterliegt das jeweilige Segment in einer Kurve ersten Grades lediglich der Auswirkung der beiden End-Kontrollpunkte. In einer Kurve zweiten Grades wirken sich drei Kontrollpunkte auf das jeweilige Segment aus, und so weiter.
- Kurven ersten Grades gehen durch alle Kurvenkontrollpunkte. In einer NURBS-Kurve ersten Grades bestimmen zwei (Grad+1)-Kontrollpunkte jedes Segment. Bei Verwendung von fünf Kontrollpunkten hat die Kurve vier Segmente.
- Kreise und Ellipsen sind Beispiele für Kurven zweiten Grades. In einer NURBS-Kurve zweiten Grades bestimmen drei (Grad+1)- Kontrollpunkte das jeweilige Segment. Bei Verwendung von fünf Kontrollpunkten hat die Kurve drei Segmente.
Die Kontrollpunkte haben eine angegliederte Zahl, die Wichtung genannt wird. Bis auf einige Ausnahmen sind Wichtungen positive Zahlen. Intuitiv sind die Wichtungen denkbar als die Schwere jedes einzelnen Kontrollpunkts. Je höher die relative Wichtung eines Kontrollpunkts, desto näher wird die Kurve an diesen Kontrollpunkt herangezogen. Wenn die Kontrollpunkte einer Kurve alle dieselbe Wichtung (normalerweise 1) haben, wird die Kurve nicht- rational genannt. Andernfalls wird die Kurve rational genannt. Das R in NURBS steht für rational und weist darauf hin, dass für eine NURBS-Kurve die Möglichkeit besteht, rational zu sein. In der Praxis sind die meisten NURBS-Kurven nicht-rational. Manche NURBS-Kurven – Kreise und Ellipsen sind herausragende Beispiele – sind immer rational. (Quelle)
5.2.6 – Bewertungsregel
Die NURBS-Bewertungsregel ist eine Formel, die mit Grad, Kontrollpunkten und Knoten[1] arbeitet. Die Formel enthält sogenannte B-Spline-Basisfunktionen die einen Parameter nimmt und einen Punktstandort erzeugt. Grad, Knoten und Kontrollpunkte sind die Parameter dieser Formel . (Quelle)
5.2.7 – Geometrische Kurvenstetigkeit
Stetigkeit ist ein wichtiges Konzept in der 3D-Modellierung. Stetigkeit ist wichtig, um visuelle Glätte wie auch sanftes Licht und Luftströmung zu erhalten. Die folgende Tabelle enthält verschiedene Stetigkeiten und ihre Definitionen:
| G0 (Positionsstetig) | Zwei miteinander verbundene Kurvensegmente |
| G1 (Tangentenstetig) | Die Richtung der Tangente am Verbindungspunkt ist für beide Kurvensegmente gleich |
| G2 (Krümmungsstetig) | Krümmungen wie auch Tangenten stimmen für beide Kurvensegmente am gemeinsamen Endpunkt überein |
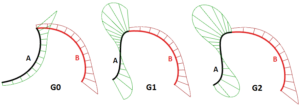
Abbildung 5.4 – Überprüfung der Kurvenstetigkeit Analyse der Krümmungsanzeige.
Krümmung ist ein bei der Modellierung von 3D-Kurven und -Flächen viel verwendetes Konzept. Krümmung wird definiert als die Änderung in der Neigung einer Tangente zu einer Kurve über eine Bogeneinheitslänge. Für einen Kreis oder eine Kugel ist dies der Kehrwert des Radius und über die gesamte Domäne hinweg konstant.
An jedem beliebigen Punkt auf einer Kurve in der Ebene ist die tangentiale Linie die Linie, die sich der Kurve durch diesen Punkt am meisten nähert. Wir können auch den besten annähernden Kreis finden, der durch diesen Punkt verläuft und tangential zur Kurve liegt. Der Kehrwert des Radius dieses Kreises ist die Krümmung der Kurve an diesem Punkt.
5.3 – Flächen
5.3.1 – Abwickelbare Fläche
Eine abwickelbare Fläche bezeichnet in der Geometrie bzw. in der Differentialgeometrie, der Kartografie und der Topologie eine Fläche, die sich ohne innere Formverzerrung aus dem Euklidischen Raum in die Euklidische Ebene transformieren/“abwickeln“ lässt. Die sich ergebende Fläche wird dann Abwicklung genannt. Anschaulich gesprochen: Ohne Stauchen und Zerren muss sich die abwickelbare Fläche glatt auf eine flache Ebene legen lassen. Bekannteste Beispiele sind Körper mit planaren Flächen (Polyeder), aber auch die Mantelflächen bestimmter dreidimensionaler Körper wie Zylinder oder Kegel. (Quelle)

Abbildung 5.5 – Abwicklung der Mantelfläche eines Zylinders
5.3.2 – Regelfläche
In der Geometrie heißt eine Fläche Regelfläche, wenn durch jeden Punkt der Fläche eine Gerade geht, die ganz in der Fläche enthalten ist. Hyperboloide und Hyperbolische Paraboloide sind auch Regelflächen.
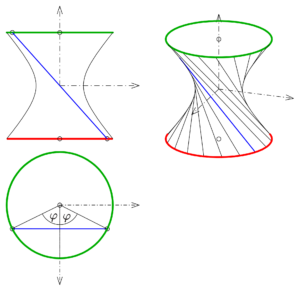
Abbildung 5.6 – Regelfläche: einschaliges Hyperboloid.
5.4 – Parametrische Flächen
5.4.1 – Flächenparameter
Eine parametrische Fläche ist eine Funktion zweier unabhängiger Parameter (meist u, v genannt) über einer zweidimensionalen Domäne.
5.4.2 – Flächendomäne
Eine Flächendomäne wird definiert als der Bereich von (u,v)-Parametern, die zu 3D- Punkten auf dieser Fläche ausgewertet werden. Die Domäne in jeder Dimension (u oder v) wird gewöhnlich als zwei reelle Zahlen beschrieben (u_min bis u_max) und (v_min bis v_max)
5.4.3 – Flächenauswertung
Die Auswertung einer Fläche auf einem Parameter innerhalb der Flächendomäne ergibt einen Punkt auf der Fläche. Bedenken Sie, dass die Mitte der Domäne (midu, midv) nicht unbedingt dem metrischen Mittelpunkt der 3D-Fläche entspricht (siehe auch Kurvendomände). Auch wird die Auswertung der u- und v-Werte, die sich außerhalb der Flächendomäne befinden, kein gutes Ergebnis erbringen.
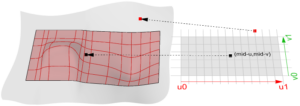
Abbildung 5.7 – NURBS-Fläche in 3D-Modellierungsraum (links). Das Flächenparameterrechteck mit Domäne, die von u0 bis u1 in der ersten Richtung und von v0 bis v1 in der zweiten Richtung reicht (rechts). Flächenauswertung.
5.4.4 – Geometrische Flächenstetigkeit
Viele Modelle können nicht anhand einer einzigen Fläche erzeugt werden. Stetigkeit zwischen verbundenen Flächen ist von Bedeutung für visuelle Glätte, Lichtreflektierung und Luftströmung.
Die folgende Tabelle enthält verschiedene Stetigkeiten und ihre Definitionen:
| G0 (Positionsstetig) | Zwei miteinander verbundene Flächen. |
| G1 (Tangentenstetig) | Die einander entsprechenden Tangenten der beiden Flächen entlang ihrer Verbindungskante sind sowohl in u- als auch v-Richtung parallel. |
| G2 (Krümmungsstetig) | Krümmungen wie auch Tangenten stimmen für beide Flächen an der gemeinsamen Kante überein. |
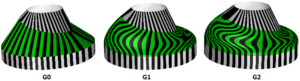
Abbildung 5.8 – Prüfung der Flächenstetigkeit mit der Lichtlinienanalyse.
5.5 – NURBS Flächen
Man kann sich NURBS-Flächen als ein Raster von NURBS-Kurven vorstellen, die in zwei Richtungen verlaufen. Die Form einer NURBS-Fläche wird durch eine Zahl von Kontrollpunkten bestimmt, sowie den Grad dieser Fläche in jede dieser beiden Richtungen (u- und v-Richtungen). NURBS-Flächen sind effizient bei der Speicherung und Darstellung von Freiformflächen mit hohem Genauigkeitsgrad. Die mathematischen Gleichungen und Details von NURBS-Flächen gehen über den Rahmen dieses Texts hinaus. Stattdessen konzentrieren wir uns lieber auf die für Designer relevantesten Eigenschaften. (Quelle)
Isolinien (Iso ist die Kurzform für isoparametrisch) sind im NURBS Modellierung, Linien mit konstantem Parameter wert, ähnlich zu einer Konturlinie. Isolinien werden beim Darstellen von NURBS Flaechen verwendet. Man kann NURBS kurven basierend auf den Isolinien von U-werten oder V-werten erzeugen.
5.5.1 – Getrimmte NURBS-Flächen
NURBS-Flächen können getrimmt oder ungetrimmt sein. Getrimmte Flächen verwenden eine darunterliegende NURBS-Fläche und geschlossene Kurven, um einen Teil dieser Fläche herauszutrimmen. Jede Fläche hat eine geschlossene Kurve, welche die äußere Kante (äußere Schleife) bestimmt, und sie kann nicht- überschneidende, geschlossene innere Kurven zur Bestimmung von Öffnungen (innere Schleifen) haben. Eine Fläche mit einer äußeren Schleife, welche die gleiche wie die ihrer darunterliegenden NURBS-Fläche ist und keine Öffnungen hat, ist was wir eine ungetrimmte Fläche nennen.
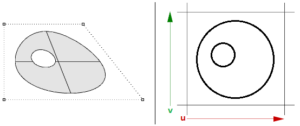
Abbildung 5.9 – Getrimmte Fläche in Modellierungsraum (links) und in Parameterrechteck (rechts).
5.5.2 – Flächenverbände
Ein Flächenverband besteht aus zwei oder mehr (möglicherweise getrimmten) miteinander verbundenen NURBS-Flächen. Jede Fläche hat ihre eigene Struktur, Parametrisierung und Isokurven-Richtungen, die nicht übereinstimmen müssen. Flächenverbände werden unter Verwendung des Begrenzungsflächenmodells ( engl. Abk. für Boundary Representation) dargestellt. Die BRep-Struktur beschreibt Flächen, Kanten und Scheitelpunkte mit Trimmdaten und Verbindung unterschiedlicher Teile. Getrimmte Flächen werden auch unter Verwendung von BRep-Datenstruktur dargestellt.
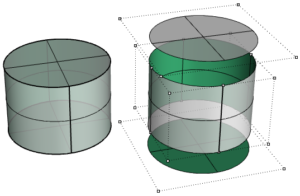
Abbildung 5.10 – Die oberen und unteres Seiten des Zylinders im folgenden Beispiel sind aus planaren Flächen getrimmt. Die Abbildung zeigt die Kontrollpunkte der darunterliegenden Flächen.
5.6 – Bildtafeln
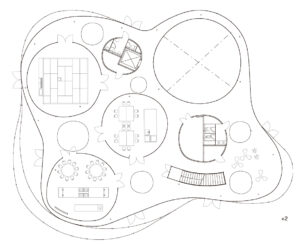
- Toyota Aizuma Hall, Aichi – Kazuyo Sejima & Associates
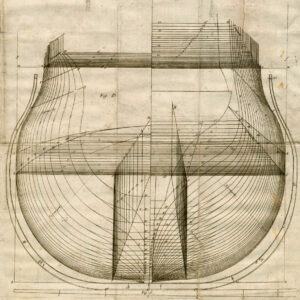
- A ship’s body plan comprised of superimposed construction geometry. Cross sections such as these recorded vessels on contractual order. The outer member (marked Fig. E/F) is the midships mould. Portions of each cross section are indexed to corresponding pieces on the reconfigurable mould. Source: William Sutherland, The Shipbuilders Assistant: or, Some Essays Towards Completing the Art of Marine Architecture (London, 1711), 82.
- Enric Ruiz-Geli created the Villa Nurbs in the coastal town Empuriabrava at the Costa Brava, Spain.
- BMW Gina, Design Chris Bangle
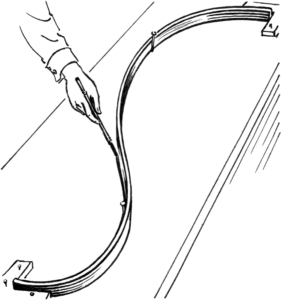
- Zeichnen einer Spline
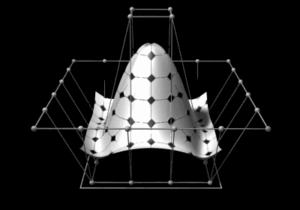
- Dreidimensionale NURBS-Flächen können komplexe, organische Formen aufweisen. Kontrollpunkte beeinflussen die Richtungen der Oberfläche.
- Autobahnkreuz, Los Angeles
- Kurven einer Achterbahn
- Knoten sind eine Liste von Zahlen mit (Grad+N-1), wobei N für die Anzahl Kontrollpunkte steht. Manchmal wird diese Zahlenliste auch Knotenvektor genannt. In diesem Zusammenhang bedeutet das Wort Vektor nicht 3D-Richtung. Für den Designer sind Knoten gewöhnlich nicht hilfreich; sie werden nur für interne Berechnungen benötigt. Aus diesem Grund sind Knoten in vielen Graphik-Design-Programmen nicht änderbar oder überhaupt sichtbar. Einige CAD Programme erlauben interaktive Änderungen an Knotenpositionen, was allerdings bedeutend weniger intuitiv ist als Änderungen an Kontrollpunkten. ↵
Non-uniform rational B-Splines (deutsch: nicht-uniforme rationale B-Splines, kurz NURBS) sind mathematisch definierte Kurven oder Flächen, die im Computergrafik-Bereich, beispielsweise im CGI oder CAD, zur Modellierung beliebiger Formen verwendet werden. NURBS sind mathematische Darstellungen, die beliebige Formen von einfachen 2D-Linien, -Kreise, -Bogen oder -Kurven bis hin zu hoch komplexen organischen 3D-Freiformflächen und -Volumenkörpern darstellen können. Aufgrund ihrer Flexibilität und Genauigkeit können NURBS-Modelle in allen Prozessen von Illustration und Animation bis hin zur Fertigung verwendet werden.
Ein Flächenverband besteht aus zwei oder mehr (möglicherweise getrimmten) miteinander verbundenen NURBS-Flächen. Jede Fläche hat ihre eigene Struktur, Parametrisierung und Isokurven-Richtungen, die nicht übereinstimmen müssen. Flächenverbände werden unter Verwendung des Begrenzungsflächenmodells (BRep engl. Abk. für Boundary Representation) dargestellt.