13.1 – Geometrische Analysen

13.1.1 – Sichtbarkeit

Ein einzelner „Isovist“ (von iso-: gleich, -vist: sicht) ist das Raumvolumen, das von einem bestimmten Punkt im Raum aus sichtbar ist, zusammen mit einer Angabe der Position dieses Punktes. Isovists sind von Natur aus dreidimensional, können aber auch in zwei Dimensionen untersucht werden: entweder im horizontalen Schnitt („Plan“) oder in anderen vertikalen Schnitten durch den dreidimensionalen Raum. Jedem Punkt im physikalischen Raum kann ein Isovist zugeordnet werden. Der Isovist ist ein Ansatz, Raum aus der Sicht einer Person in einer Umgebung zu beschreiben. Es bezieht sich auf das Polygon, welches entsteht durch die Begrenzung aller (360°) von einem Punkt aus gesendeten Strahlen an den umliegenden Hindernissen. (Quelle en)

Beispiel

Die Grenzform eines Isovisten kann je nach Standort in einem Raum variieren oder nicht. Wenn der Raum konvex ist (z. B. ein Rechteck oder ein Kreis), dann ist die Grenzform aller Isovisten in diesem Raum gleich; ebenso deren Volumen (oder deren Fläche, wenn wir im Plan denken). Wenn der Raum jedoch nicht konvex wäre (z. B. ein L-förmiger oder unterteilter Raum), dann gäbe es viele Isovisten, deren Volumen (Fläche) kleiner wäre als das des gesamten Raums, und vielleicht einige, die das ganze Zimmer wären; und viele hätten unterschiedliche, vielleicht einzigartige Formen: groß und klein, schmal und breit, zentrisch und exzentrisch, ganz und nur teilweise.

Man kann sich die Isoviste auch als das von einer Punktlichtquelle beleuchtete Raumvolumen vorstellen. Es kann auch in der digitalen 3D-Umgebung als der Bereich betrachtet werden, der nicht im Schatten einer einzelnen Punktlichtquelle liegt.

Es wird im Bereich der Architektur zur Analyse von Gebäuden und Stadtgebieten verwendet (u.a. als eine von einer Reihe von Methoden, die in der Space Syntax verwendet werden).

Abbildung 13.1 – Die blaue Fläche ist der Isovist der vom Zentrum des Kreises gesehen werden kann.

13.1.2 – Sonne & Schatten

In der Darstellenden Geometrie verwendet man Schattenkonstruktionen um die Darstellung räumlicher Objekte realistischer zu machen oder um Beleuchtungsprobleme schon in der Planungsphase diskutieren zu können. Wenn eine Parallelprojektion oder eine Zentralprojektion eines Objektes, z. B. eines Hauses, vorliegt, so ist es relativ einfach, Schatten auf eine horizontale Ebene (Standebene) sowohl von parallelem (Sonne) als auch zentralem (Lampe) Licht zu konstruieren. In allgemeineren Fällen (Schatten auf Ebenen, die von der Standebene verschieden sind) kann man den Schatten zunächst in Grund- und Aufriss, eventuell mit Hilfe der Durchstoßpunktmethode, konstruieren und dann in das Bild einzeichnen. (Quelle)

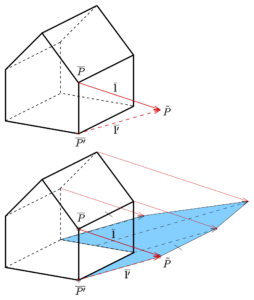
Abbildung 13.2 – Parallelprojektion: Schatten bei parallelem Licht

13.1.2.1 – Schattenwurf von Hochhäusern (Kanton ZH und andere)

Hochhäuser dürfen ihre Nachbarschaft insbesondere durch Schattenwurf nicht wesentlich beeinträchtigen. So dürfen bewohnte Gebäude oder bebaute sowie überbaubare Flächen in Wohnzonen an den mittleren Wintertagen nicht länger als drei Stunden beschattet werden.

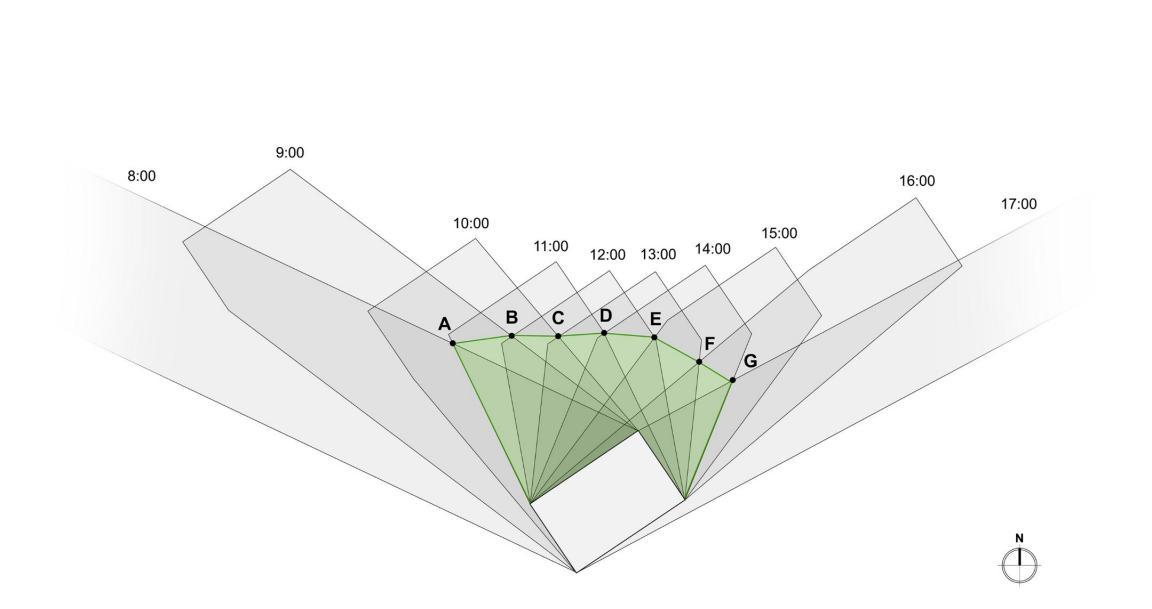
Abbildung 13.3 – Das gesuchte Schattendiagramm ergibt sich durch das Verbinden der Schnittpunkte der jeweils drei Stunden auseinanderliegenden Schatten.

13.2 – Netzwerk Analysen

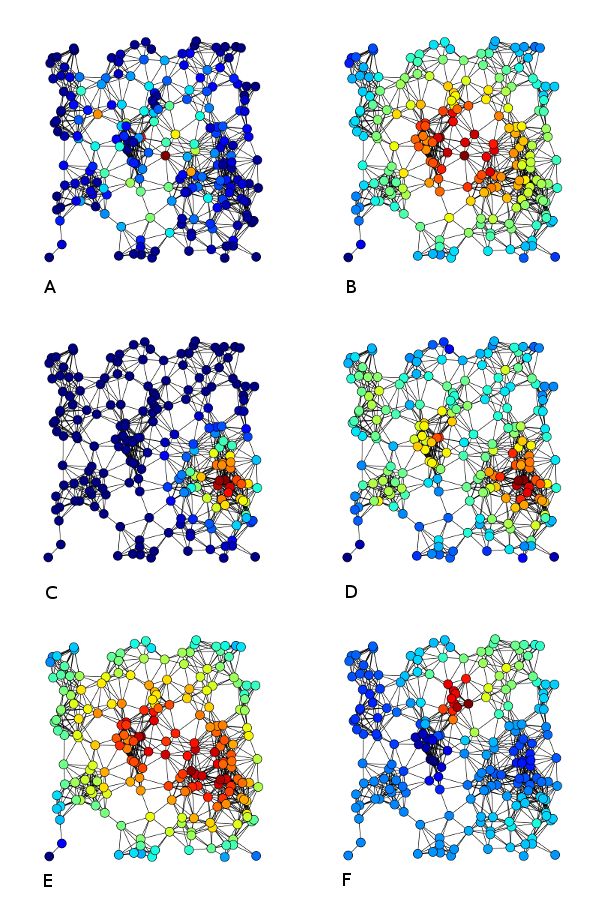
Abbildung 13.4 – Zentralitätsberechnung A) Betweenness, B) Closeness, C) Eigenvector, D) Degree, E) Harmonic und F) Katz.

Der Begriff Space Syntax umfasst eine Reihe von Theorien und Techniken zur Analyse räumlicher Konfigurationen. Es wurde von Bill Hillier, Julienne Hanson und Kollegen am The Bartlett, University College London in den späten 1970er bis frühen 1980er Jahren konzipiert, um Einblicke in die gegenseitig konstruktive Beziehung zwischen Gesellschaft und Raum zu gewinnen. Mit der Entwicklung der Space Syntax hat sich herausgestellt, dass bestimmte Maße mit dem menschlichen Raumverhalten korrelieren. Space Syntax wurde daher verwendet, um wahrscheinliche Auswirkungen des architektonischen und städtischen Raums auf die Benutzenden vorherzusagen.

13.3 – Simulation

Die oder Simulierung bezeichnet die Nachbildung von realen Szenarien oder der Analyse von Systemen, deren Verhalten für die theoretische, formelmäßige Behandlung zu komplex sind. Bei der Simulation werden Experimente oder Trainings an einem Modell durchgeführt, um Erkenntnisse über das reale System zu gewinnen. Dabei wird das Modell unterschiedlichen Einflussgrößen ausgesetzt. Letzteres stellt eine Abstraktion des zu simulierenden Systems dar (Struktur, Funktion, Verhalten). (Quelle)

13.4 – Physics Engine

Eine ist eine Funktionseinheit der Informationstechnologie, die zur Simulation physikalischer Prozesse sowie der Berechnung objektimmanenter Eigenschaften (z. B. Impuls) dient. Ziele sind eine Vereinfachung der Programmierung und die Vermittlung von realistischen Bewegungsabläufen in einer 3D-Ansicht, beispielsweise soll eine realistische „Spielphysik“ erzielt werden. Hauptanwendungsgebiete sind moderne Computerspiele und Simulationssoftware, sowie in Filmstudios zur Erzeugung von Spezialeffekten.

Dabei geht es nicht immer unbedingt um physikalische Exaktheit, sondern variert anwendungsspezifisch. Dies liegt oft an der immensen Komplexität der auf physikalischen Prozessen basierenden Berechnungen. Da in solchen Fällen meist ein Anspruch auf Echtzeitfähigkeit besteht, geht Effizienz vor Exaktheit.

Physiksengines lassen sich je nach Methode in folgende Kategorien unterteilen:

Physik starrer Körper (rigid body mechanics)
nicht elastische Physik mit Deformationen (soft body dynamics)
Masse-Feder Modelle (spring dynamics) u. a. als Grundlage der Simulation von Seilen und Stoff (rope bzw. cloth)
Partikelsysteme u. a. als Grundlage der Simulation von Flüssigkeiten (fluid dynamics) und Feuer

(Quelle)

13.5 – Partikel

Ein Partikelsystem ist eine Funktion im Bereich der Computeranimation, mit der sich eine große Anzahl von Objekten animieren lässt. Partikelsysteme werden beispielsweise eingesetzt, um Feuer-, Rauch- oder Explosionseffekte zu simulieren.

Bei einem Partikelsystem werden von einem so genannten Emitter Partikel ausgestoßen, deren Bewegung über zahlreiche Parameter beeinflusst werden kann^[1]. Diese sind unter anderem:

Ausstoßgeschwindigkeit
Lebensdauer
Dämpfung (das Partikel wird mit der Zeit langsamer)
Anzahl der Partikel im Gesamtsystem
Aufteilung von Partikeln in eine bestimmte Zahl weiterer Partikel nach einer bestimmten Zeitspanne (Multiplikation)
eine Zufälligkeit des Verhaltens
Krafteinflüsse auf die Partikel

Die Partikel sind zunächst nur logische Elemente, denen grafische Eigenschaften zugewiesen werden müssen, damit sie sichtbar werden. Zum Beispiel kann jedes Partikel durch ein geometrisches Objekt ersetzt werden, wodurch sich Schwärme, Asteroidenfelder und Ähnliches darstellen lassen (Mitte im Bild). Mit entsprechenden Materialzuweisungen können Partikelsysteme auch eingesetzt werden, um Rauch, Nebel oder Feuer darzustellen (links im Bild).

Weitergehende Partikelsysteme können auch auf andere Objekte reagieren, von denen sie je nach Einstellung angezogen oder abgestoßen werden oder an denen sie abprallen (physikalische/ereignisbasierende Verhaltensweisen). Durch die Darstellung der Bewegungspfade der einzelnen Partikel werden Haare, Plüsch, Grasflächen und ähnliche Strukturen realisiert. (Quelle)

Abbildung 13.5 – Stellt Verschiedene Anwendungen von Partikelsystemen bei 3D-Programmen dar.

13.6 – Agenten

Bei einem oder MAS handelt es sich um ein System aus mehreren gleichartigen oder unterschiedlich spezialisierten handelnden Einheiten, Software-Agenten, die kollektiv ein Problem lösen.

Multiagentensysteme existieren sowohl in der Biologie (natürliche Multiagentensysteme) als auch in der Technik. Eine Beispielfamilie biologischer Multiagentensysteme stellen Ameisenstaaten dar. Einige der in Ameisenstaaten ablaufenden Algorithmen (Ameisenalgorithmen) stellen heuristische Lösungsverfahren für komplexe Optimierungsaufgaben dar und sind neben ihrem grundsätzlichen Interesse innerhalb der Theoretischen Biologie auch ein Vorbild bei der Optimierung technischer Prozesse. Man spricht auch von verteilter, im Bereich der Technik von künstlicher Intelligenz oder DAI (distributed artificial intelligence).

Außerhalb Europas, insbesondere in den USA, hat sich für MAS die Bezeichnung Agent-based Modeling bzw. Simulation (ABM) durchgesetzt. (Quelle)

13.7 – Emergenz

(lateinisch emergere „Auftauchen“, „Herauskommen“, „Emporsteigen“) bezeichnet die Möglichkeit der Herausbildung von neuen Eigenschaften oder Strukturen eines Systems infolge des Zusammenspiels seiner Elemente. Dabei lassen sich die emergenten Eigenschaften des Systems nicht – oder jedenfalls nicht offensichtlich – auf Eigenschaften der Elemente zurückführen, die diese isoliert aufweisen. Das Phänomen der emergenten Selbstorganisation wird als Autopoiesis bezeichnet. (Quelle)

by KAISERSROT

13 Analyse und Simulation