1.1 – Digitale Signale und Binärcode

Damit Architekten die gebaute Umwelt am Computer planen und modifizieren können, muss die physische reale Welt in Signale übersetzt werden, die Computer verstehen. Diese Signale sind numerische Grössen (Zahlen), und Instruktionen, wie diese Daten verarbeitet werden sollen.

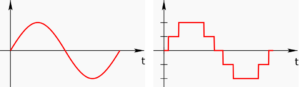
Abbildung 1.1 – Kontinuierliche (analoge) und diskrete (digitale) Signale

Die Werte in der realen Welt – z.B. physikalische Grössen wie Temperatur, Luftdruck, Wasserstand, eine Tonfrequenz oder Lautstärke, oder auch eine Position im Raum – sind stufenlos, kontinuierlich an jeder beliebigen Stelle und Zeitpunkt messbar. Man nennt dies ein analoges Signal, und Quecksilberthermometer oder -barometer sind Beispiele für analoge Sensoren.

Ein analoges Signal ist eine physikalische Größe, die im Verlauf der Größe (Amplitude) als auch im zeitlichen Verlauf kontinuierliche Werte annehmen kann.

Computer können nun diese analogen Signale mit einer vorbestimmten Auflösung (z.B. Temperatur auf 1/10° oder eine Nachkommastelle präzise) und in vorbestimmten Zeitintervallen (z.B alle 10 Minuten oder alle 5 Millisekunden) abfragen und als Zahl speichern.

Ein digitales Signal (digitus: Finger, lat.) ist eine physikalische Größe, die nur bestimmte diskrete Werte annehmen kann. Die Werte entsprechen der Anzahl der vordefinierten Zustände. Werden zwei Zustände definiert (0 und 1), dann handelt es sich um binäre (digitale) Signale.

Computer arbeiten mit winzig kleinen Einheiten genannt „bit“. Das Wort hat nicht nur die gängige englische Bedeutung von „ein wenig“, sondern ist im Computer-Jargon auch der Zusammenzug aus „binary“ und „digit„. Digit kommt davon dass es einen Wert anzeigt. „Binary“ (dt. binär) kommt von bi = 2. Ein bit kann also 2 Werte annehmen, 0 oder 1, an oder aus, wahr oder falsch.

Um mehr Zahlen anzeigen zu können braucht man mehr Bits. Mit 3 Bits kann man 8 verschiedene Zahlen anzeigen (2³):

000 = 0 / 001 = 1 / 010 = 2 / 011 = 3
100 = 4 / 101 = 5 / 110 = 6 / 111 = 7

Um ein digitales Thermometer zu bauen, das von -60° bis +60° anzeigen kann braucht man also 7 Bits: 6 für die 60 (64=2⁶) Zahlen, und 1 für das Vorzeichen (+ oder -).

Ein Binärcode ist ein Code, in dem Informationen durch Sequenzen von zwei verschiedenen Symbolen (zum Beispiel 1/0 oder wahr/falsch) dargestellt werden.

Abbildung 1.2 – Binäre Darstellung des Wortes „Wikipedia“

Alle 0/1-Zeichenketten in dem Wort Wikipedia fangen mit der Sequenz 01 an. Dies sagt dem Computer, dass was danach kommt ein Buchstabe ist, und die resultierende Zahl gemäss einer definierten Tabelle einem Zeichen entspricht.

Im weiteren Sinne war Leibniz wegbereitend für die Rechenmaschine im heutigen Sinne, den Computer. Er entdeckte, dass sich Rechenprozesse viel einfacher mit einer binären Zahlencodierung durchführen lassen, und ferner, dass sich mittels des binären Zahlencodes die Prinzipien der Arithmetik mit den Prinzipien der Logik verknüpfen lassen (siehe De progressione Dyadica, 1679; oder Explication de l’Arithmetique Binaire, 1703). Die hier erforschten Prinzipien wurden erst 230 Jahre später in der Konstruktion von Rechenmaschinen eingesetzt (z. B. bei der Zuse Z1). Leibniz hatte beim Bau einer Rechenmaschine, anders als frühere Erfinder, eher philosophische Motive. Mit dem viel bemühten Zitat, es sei „ausgezeichneter Menschen unwürdig, gleich Sklaven Stunden zu verlieren mit Berechnungen“, wird eine Grenze zwischen Mensch und Maschine gezogen. Dem Erfindergeist (Freiheit, Spontaneität und Vernunft) als das spezifisch Menschliche wird das Mechanische der technisch-natürlichen Kausalität gegenübergestellt. (Quelle)

Binärcodes bilden auf Grund ihrer Einfachheit in aller Regel die Grundlage für die Verarbeitung digitaler Informationen und werden deshalb häufig im Zusammenhang mit deren Verarbeitung genannt; „Computer funktionieren mit diesem Code“.

Viele der Binärcode-Arten sind im Gebiet der Informationstechnik entstanden und werden dort verwendet; der Ausdruck „Binärcode“ wird im Computer-Sprachgebrauch auch als Synonym für Maschinencode, Maschinenprogramm oder Maschinensprache verwendet.

1.2 – Vom Jacquard Webstuhl zur Rechenmaschine

Als Jacquardwebstuhl bezeichnet man den von Joseph-Marie Jacquard weiterentwickelten Webstuhl. Beim ursprünglichen Jacquardwebstuhl wurden die Platinenbewegungen durch Lochkarten gesteuert. Dies war eine der ersten bekannten Anwendungen der Lochkartentechnik überhaupt. Zur Hardware, dem Webstuhl, haben wir hier also erstmals eine Software, die Lochkarte, die die Hardware steuern kann. Die meisten neueren Einrichtungen arbeiten mit elektromagnetischer Übertragung der vom Computer gegebenen Steuerungsimpulse. Diese Verwendung von austauschbaren Lochkarten zur Steuerung einer Abfolge von Vorgängen gilt als wichtiger Schritt in der Geschichte der Computerhardware und hat die Analytical Engine von Charles Babbage inspiriert. (Quelle)

Die Analytical Engine (englisch für Analytische Maschine) ist der Entwurf einer mechanischen Rechenmaschine für allgemeine Anwendungen. Sie stammt von dem britischen Mathematikprofessor Charles Babbage (1791–1871) und stellt einen wichtigen Schritt in der Geschichte des Computers dar. Als Programme gibt es tabellarische Darstellungen; ein Satz von 1837/38 ist erhalten und enthält bereits das Beispiel für die Auflösung eines linearen Gleichungssystems, wie es von Luigi Federico Menabrea 1842 und Ada Lovelace 1843 veröffentlicht wurde; von letzterer ist wohl das Beispiel der Berechnung der Bernoulli-Zahlen. (Quelle)

Eine Turingmaschine ist ein mathematisches Modell der theoretischen Informatik, das eine abstrakte Maschine definiert. Bei diesem Rechnermodell werden nach festgelegten Regeln Manipulationen von Zeichen vorgenommen. Die Turingmaschine ist benannt nach dem britischen Mathematiker Alan Turing, der sie 1936/37 einführte. Turingmaschinen machen die Begriffe des Algorithmus und der Berechenbarkeit mathematisch fassbar, das heißt, sie formalisieren diese Begriffe und bilden eines der Fundamente der Theoretischen Informatik. (Quelle)

Abbildung 1.3 – 1-Band-Turingmaschine: abstraktes Modell eines Rechners, der mit nur drei Operationen (Lesen, Schreiben und Kopf Bewegen) sämtliche berechenbare Probleme lösen kann

1.3 – Bildtafeln