Geometrie steckt im Kern des architektonischen Entwurfsprozesses. Sie ist omnipräsent, von den ersten Schritten der Formfindung bis zur eigentlichen Konstruktion. Moderne Konstruktionsgeometrie bietet eine Reihe von Werkzeugen für effizientes Entwerfen, Analyse und die Herstellung komplexer Formen. Das führt zu neuen Herausforderungen, sowohl in der Architektur als auch in der Geometrie. Architekturgeometrie ist daher als integrative Forschungsaufgabe zu sehen, die an der Grenze zwischen angewandter Geometrie und Architektur angesiedelt ist.
At best there is something desperately uncommunicative about it, something more than a little removed from the rest of experience to set against its giant claim of truth. Flaubert, in The Dictionary of Accepted Ideas, defines a geometrician as „travelling on strange seas of thought-alone.“
And when Joseph Conrad wished to characterize the futile effort of concentration made by the earnest but mentally retarded youth Stevie in The Secret Agent, he would describe him as „seated very good and quiet at a deal table, drawing circles, circles, circles; innumerable circles, concentric, eccentric, a coruscating whirl of circles that by their tangled multitude of repeated curves, uniformity of form, and confusion of intersecting lines suggested a rendering of cosmic chaos, the symbolism of a mad art attempting the inconceivable.“ – Robin Evans, The projective cast
4.1 – Entwicklung der Darstellende Geometrie
Bei der systematischen Errichtung von Bauwerken spielen Pläne mit konkreten Vorgaben eine wichtige Rolle. Schon im Altertum wurden Grund- und Aufrisse verwendet. Der älteste schriftliche Beleg dafür ist das Werk Zehn Bücher über Architektur des römischen Baumeisters Vitruvius. Aber erst Albrecht Dürer (1471–1528) schrieb in der Frühen Neuzeit das erste wirkliche Lehrbuch der Darstellenden Geometrie: Underweysung mit dem Zirkel und Richtscheydt[2] (Nürnberg 1525). Gaspard Monge (1746–1818) führte in seinem Buch Geometrie descriptive[3] zum ersten Mal die strenge Zuordnung von Grund- und Aufriss ein, um räumliche Probleme zeichnerisch zu lösen. Die Grundaufgaben der Darstellenden Geometrie sind dort schon in der noch heute gebräuchlichen Fassung zu finden. (Quelle)
4.1.1 – Die Trennung von Planung und Ausführung
Alberti
Auffallend an der Architekturtheorie Albertis ist vor allem ihre erstaunliche Modernität. Es geht um die neue Rolle des Architekten als reiner Planer mit eigenem, nicht mehr handwerklich geprägtem Ausbildungsgang. (Quelle) Der Architekt, den sich Alberti vorstellte, sollte sich in der Malerei und in der Mathematik auskennen. Dies hatte zwar schon Vitruv gefordert, aber Alberti bezog sich hier auf das Kernstück seiner Abhandlung über die Malerei, nämlich auf die Zentralperspektive, die für den Architekten genauso wichtig sei wie für den Maler, da er mit ihrer Hilfe die Wirkung des Gebäudes abschätzen und berechnen könne.
Allerdings handelt es sich bei dem von Alberti anvisierten Architekten um eine andere species als sie aus der baumeisterlichen Praxis des Mittelalters bekannt war. Albertis Architekt ist kein Praktiker, sondern ein Entwerfer, der sich als Gelehrter versteht. Seine Bemerkungen über seine eigene Stellung dokumentieren, dass er im architectus eine intellektuelle Autorität sah, der für die Ausführung ein Baumeister (faber) zur Seite stand, ähnlich wie man dies in Andrea Pisanos Reliefs am Campanile des Florentiner Doms sehen kann, in denen der Architekt in vornehmer Kleidung in seinem Arbeitszimmer (studiolo) sitzt, während der Baumeister die Vorgänge auf der Baustelle unter Kontrolle hält. Diesem Muster war das Verhältnis zwischen Architekt und Baumeister verpflichtet, das Albertis eigene Bauvorhaben kennzeichnet. (Quelle)
In den frühesten Zeichnungen wurde die anschauliche perspektivische (dreidimensionale) Darstellung – anfänglich in primitiver und ab der Renaissance in korrekter Weise – benutzt.[1] Weil sie relativ hohe Anforderungen an die Begabung der Zeichner stellt, ging man bei Beginn der Industrialisierung (18. Jahrhundert) auf zweidimensionale Abbildungen der Objekte in rechtwinkliger Parallelprojektion (Orthogonalprojektion) über. Die Kanten und Symmetrie-Linien der meisten technischen Gegenstände sind untereinander rechtwinklig angeordnet. Man kann ihnen ein rechtwinkliges Koordinatensystem überlagern und von ihnen Ansichten (Vorder-/Rückansicht, Seitenansicht von rechts/links und Drauf-/Untersicht) in je einer Richtung der Koordinatenachsen erzeugen. Die in den drei Koordinatenebenen liegenden Flächen werden unverzerrt abgebildet. Bei der angewendeten Parallelprojektion ist der Abbildungsmaßstab unabhängig davon, welchen Abstand eine Objektebene vom Betrachter hat; alle Längen sind maßstabgleich dargestellt. Nachteilig ist, dass sich der Betrachter die Geometrie des Körpers aus mehreren Ansichten (und gegebenenfalls Schnitten bei Körpern mit Hohlräumen) vorstellen muss (setzt räumliches Vorstellungsvermögen voraus).(Quelle)
4.2 – Projektionen
Vor der Einführung von Computergrafik (engl. Computer-graphics) war Wissen um Projektionstechniken nötig. Heute wird das von Computern in Echtzeit durchgeführt. Um die digitalen Techniken möglichst gut zur Visualisierung nutzen zu können, ist dennoch ein grundlegendes Verständnis nötig. (Helmut Pottmann, Architectural Geometry). In der Darstellenden Geometrie bedient man sich im Wesentlichen zweier Abbildungsverfahren. Dabei werden Punkte und Kurven eines Objektes mit Hilfe von Strahlen (Geraden) auf eine Bildtafel (Ebene) projiziert:
4.2.1 – Parallelprojektion
Die Abbildungsstrahlen sind parallel, wie z. B. beim Sonnenlicht. Dabei unterscheidet man noch die beiden Fälle:
- Die Strahlen stehen senkrecht auf der Bildtafel (senkrechte Parallelprojektion oder Orthogonalprojektion oder Normalprojektion).
- Die Strahlen stehen nicht senkrecht zur Bildtafel (schiefe oder schräge Parallelprojektion).
Parallelprojektionen werden wegen ihrer Teilverhältnistreue (Teilverhältnisse auf Geraden bleiben invariant) gerne von Ingenieuren verwendet. Der Spezialfall Vogelperspektive ist eine schiefe Parallelprojektion, die insbesondere zur Veranschaulichung von Stadtplänen verwendet wird. Sie lässt sich relativ einfach von Hand herstellen. Parallelprojektionen lassen sich schnell als axonometrische Bilder oder bei umfangreicheren Objekten mit Hilfe des Einschneideverfahrens herstellen. Für fast alle Konstruktionen in der Darstellenden Geometrie verwendet man Grund- und Aufriss eines Objektes. Das sind senkrechte Parallelprojektionen auf eine horizontale (Grundriss) bzw. senkrechte Ebene (Aufriss) (s. Zweitafelprojektion). Durch sie ist (mit den entsprechenden Bezeichnungen) ein Objekt räumlich eindeutig beschrieben. (Quelle)
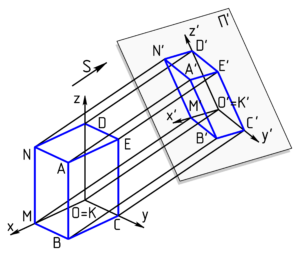
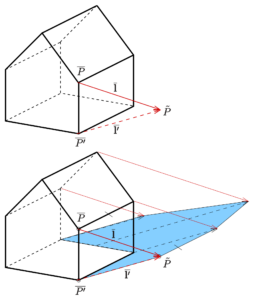
Abbildung 4.2 – Parallelprojektion
4.2.2 – Zentralprojektion
Die Grundlagen der Zentralprojektion waren schon den Griechen und Römern bekannt. Aber erst in der Renaissance wurde diese Art der Darstellung räumlicher Gegebenheiten durch die Malerei wiederentdeckt und zur Blüte weiterentwickelt. Siehe hierzu De pictura von Leon Battista Alberti (1404). Die Meister dieser Zeit waren Albrecht Dürer (1471–1528), Leonardo da Vinci (1452–1519) und Michelangelo (1475–1564). Alle Abbildungsstrahlen gehen durch einen Punkt, dem Projektionszentrum oder Augpunkt. Bei Parallelprojektion sind die Bilder paralleler Geraden i. A. wieder parallel. Bei Zentralprojektionen schneiden sich die Bilder paralleler Geraden i. A. in einem Punkt, dem Fluchtpunkt des Parallelbüschels. (Quelle)
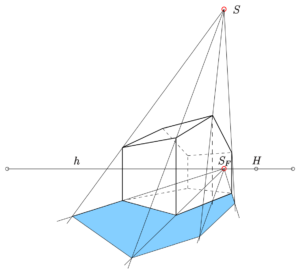
Abbildung 4.3 – Zentralprojektion
4.3 – Koordinatensysteme
Abbildung 4.4 – 1-Dimensionales Koordinatensystem
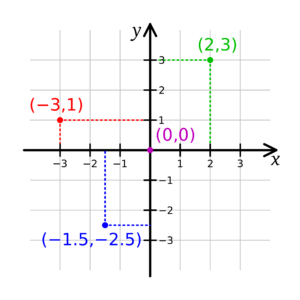
Abbildung 4.5 – 2-Dimensionales Koordinatensystem
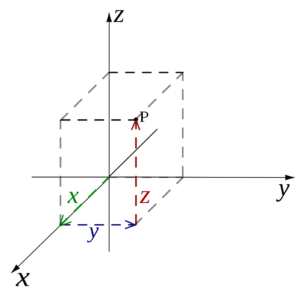
Abbildung 4.6 – 3-Dimensionales kartesisches Koordinatensystem
Eines der bekanntesten Beispiele für ein Koordinatensystem ist das kartesische Koordinatensystem. In der Ebene werden zwei Senkrechte gewählt und die Koordinaten eines Punktes als die vorzeichenbehafteten Abstände zu den Geraden aufgefasst.
In drei Dimensionen wählt man drei zueinander orthogonale Ebenen und die drei Koordinaten eines Punktes sind die vorzeichenbehafteten Abstände zu jeder der Ebenen. Es ist nach dem latinisierten Namen Cartesius des französischen Mathematikers René Descartes benannt, der das Konzept der „kartesischen Koordinaten“ bekannt gemacht hat.[3] Je nach Anordnung der Koordinatenachsen kann das dreidimensionale Koordinatensystem ein Rechts- oder ein Linkssystem sein.

Abbildung 4.7 – In Rhinos rechtshändig ausgelegtem System wird die Richtung von a × b durch die Dreifingerregel bestimmt (a = Zeigefinger, b = Mittelfinger und a × b = Daumen).
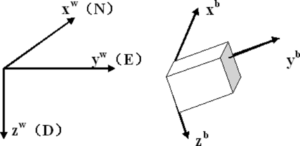
Abbildung 4.8 – Lokales Koordinatensystem
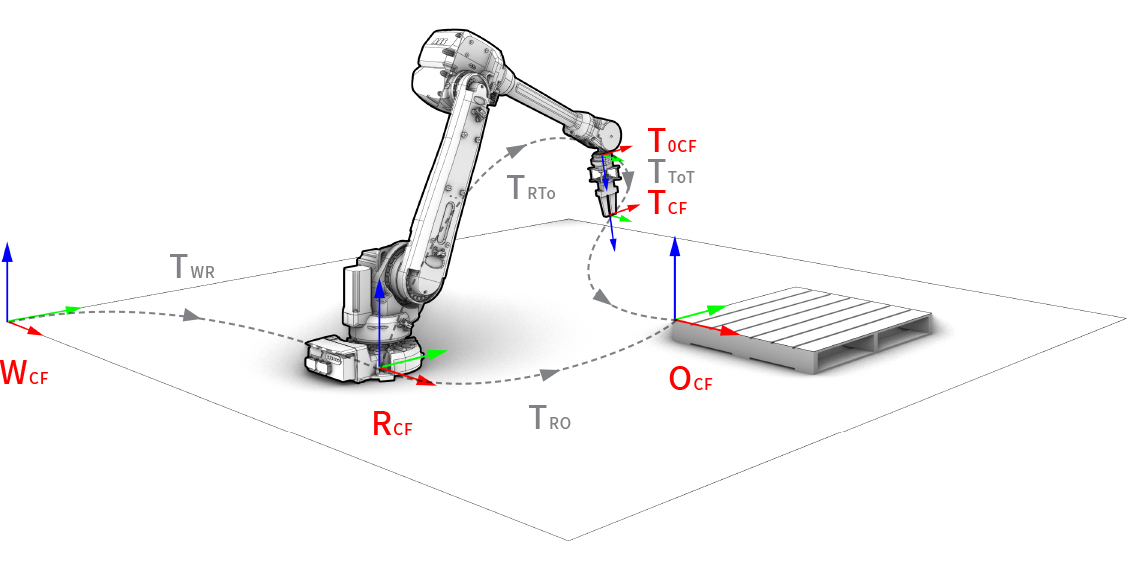
Abbildung 4.9 – Koordinatensysteme eines Roboters
4.3.0.1 – Kartesisches Koordinatensystem
4.3.0.2 – Polares Koordinatensystem
4.4 – Vektoren
Ein Vektor im n-dimensionalen Raum ist ein geordneter Satz von n reellen Zahlen. In der Ebene ist n=2, im Raum ist n=3 usw. Ein Vektor hat dadurch eine Richtung und eine Länge. Man kann dadurch z.B. physikalische Grössen darstellen, wie etwa die Fahrtrichtung und Geschwindigkeit eines Fahrrades, oder die beschleunigende Kraft der Erdanziehung auf einen fallenden Apfel.
4.4.1 – Vektoren im Vergleich zu Punkten
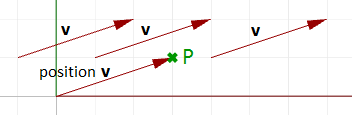
Vektoren und Punkte sollten nicht verwechselt werden. Es handelt sich dabei um sehr verschiedene Konzepte. Wie bereits erwähnt, stellen Vektoren eine Entität mit einer Richtung und Länge dar, während Punkte einen Standort anzeigen. Norden als Richtung ist zum Beispiel ein Vektor, während der Nordpol ein Standort (Punkt) ist.
Angenommen, wir haben einen Vektor und einen Punkt mit den gleichen Komponenten, etwa:
v = <3,1,0>
P = (3,1,0)
Man sagt hier, v sei der „Ortsvektor“ von P, also in welche Richtung und wie weit muss etwas sich vom Ursprung (0,0,0) weg bewegen, um den Standort P zu erreichen.
Dann können wir Vektor und Punkt folgendermaßen zeichnen:
Ein Einheitsvektor ist ein Vektor, dessen Länge einer Einheit entspricht.
Eine Möglichkeit zum Definieren einer Ebene besteht, einen in der Ebene liegenden Punkt und einen Vektor, der sich rechtwinklig zur Ebene befindet, festzulegen. Dieser Vektor wird üblicherweise als der Normalenvektor zu dieser Ebene bezeichnet.
4.5 – Transformationen
Transformationen bezieht sich auf Operationen wie das Verschieben (auch Versetzen genannt), Drehen und Skalieren von Objekten. Befehle zur Transformation eines Objekts bezüglich Größe, Form, Position oder Ausrichtung. Die meisten Transformationen behalten die Parallelbeziehung der Geometrieteile zueinander bei. Kollineare Punkte, welche auf einer Gerade liegen, bleiben zum Beispiel auch nach der Transformation kollinear. Auch Punkte auf einer Ebene bleiben nach der Transformation koplanar. Diese Art von Transformation wird auch affine Transformation genannt.
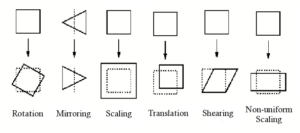
Abbildung 4.11 – verschiedene affine Transformationen
4.6 – Constructive Solid Geometry
Constructive Solid Geometry (CSG) oder konstruktive Festkörpergeometrie ist eine Technik zum Modellieren von Körpern, die u. a. in der 3D-Computergrafik und bei CAD-Programmen genutzt wird. Constructive Solid Geometry ermöglicht einem Designer einen komplex geformten Körper zu erzeugen, indem er mittels boolesche Operatoren verschiedene Grundkörper zu einem neuen Körper kombiniert. Mit CSG lassen sich durch geschickte Verknüpfung mittels Kombinationsoperationen (Union, Subtraction, Intersection) aus einfachen Grundkörpern beliebig detaillierte Objekte erstellen. (Quelle)
In der Mathematik ist eine boolesche Algebra eine spezielle algebraische Struktur, die die Eigenschaften der logischen Operatoren UND, ODER, NICHT sowie die Eigenschaften der mengentheoretischen Verknüpfungen Durchschnitt, Vereinigung, Komplement verallgemeinert. Die boolesche Algebra ist die Grundlage bei der Entwicklung von digitaler Elektronik und wird dort als Schaltalgebra, etwa bei der Erstellung von Schaltnetzen durch logische Schaltungen, angewandt. Sie wird in allen modernen Programmiersprachen zur Verfügung gestellt.[1] Die Operatoren der logischen Verknüpfung werden Boolesche Operatoren genannt. Mit Hilfe der logischen Verknüpfungen lassen sich aus einfacheren Aussagen kompliziertere Aussagen zusammensetzen. Praktische Anwendung finden die logischen Verknüpfungen unter anderem als Suchoperatoren bei Datenbanken, Anfragen an Suchmaschinen, aber auch in der Constructive Solid Geometry. (Quelle)
Die Basisobjekte, aus denen CSG-Körper hervorgehen, nennt man Primitive (vgl. Grafisches Primitiv). Typischerweise handelt es sich dabei um Körper, deren Oberfläche mittels einer relativ einfachen mathematischen Formel beschrieben werden kann, wie z. B. Würfel, Zylinder, Prismen, Pyramiden, Kugeln oder Ringe. Die Menge der möglichen Primitive wird gewöhnlich von der verwendeten Software begrenzt. Einige Software-Pakete erlauben CSG auf gekrümmten Objekten (prozedurale oder parametrische Oberflächen), während andere nur auf polygonalen Meshes (Dreiecksnetze) arbeiten. Der prozedurale oder parametrische Ansatz erlaubt eine mathematisch exakte Berechnung und Repräsentation der Körper, während Meshes immer nur eine mehr oder weniger ungenaue Annäherung an die Wirklichkeit sind. (Quelle)
Ein komplexer Körper wird von Primitiven erzeugt, die durch Operationen verknüpft sind. Gewöhnlich handelt es sich dabei um boolesche Operationen auf Mengen: Vereinigung (Union, ), Differenz (Difference, ) und Schnitt (Intersection, ). Folgende Abbildung zeigt die Wirkung der Operatoren exemplarisch an der Verknüpfung von Würfel mit Kugel:
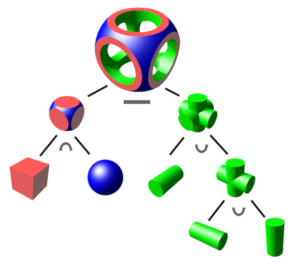
Abbildung 4.15 – CSG-Objekte können durch Binärbäume dargestellt werden, wobei Blätter Primitive darstellen und Knoten Operationen darstellen. In dieser Abbildung sind Knoten für Schnittmenge, für Vereinigung und für Unterschied aufgeführt.
4.7 – Platonische Körper
Die Platonischen Körper (nach dem griechischen Philosophen Platon) sind die Polyeder mit größtmöglicher Symmetrie. Jeder von ihnen wird von mehreren deckungsgleichen (kongruenten) ebenen regelmäßigen Vielecken begrenzt. Eine andere Bezeichnung ist reguläre Körper (von lat. corpora regularia).[1][2] Es gibt fünf platonische Körper. Ihre Namen enthalten die griechisch ausgedrückte Zahl ihrer begrenzenden Flächen und eder als Abwandlung des griechischen Wortes ἕδρα (hedra) (s. auch Polyeder), deutsch (Sitz-)Fläche. Vollkommen regelmäßige Körper. Ihre Oberflächen bestehen aus gleich großen, gleichseitigen und gleichwinkligen Vielecken. (Quelle)
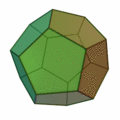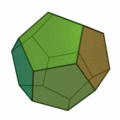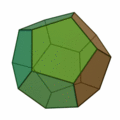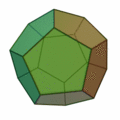

4.8 – Bildtafeln
- VitraHaus, Herzog & de Meuron, 2010
- Zeitz Mocaa Museum 2016, Thomas Heatherwick
- Kirche Saint-Marie-de-la Visitation, Francois Mansart
- Linienzeichnung, Daniel Libeskind
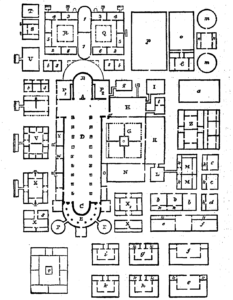
- St. Galler Klosterplan (Reichenau, frühes 9. Jahrhundert)
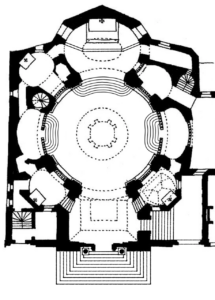
- Louis Kahn’s National Assembly Building of Bangladesh
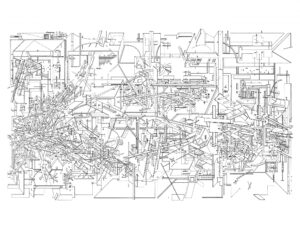
- Peter Eisenman – Transformations, Decompositions, Critiques
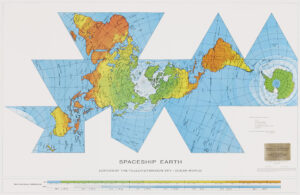
- Buckminster Fuller, Dymaxion Karte
 ),
),  ) und
) und  ). Folgende Abbildung zeigt die Wirkung der Operatoren exemplarisch an der Verknüpfung von Würfel mit Kugel:
). Folgende Abbildung zeigt die Wirkung der Operatoren exemplarisch an der Verknüpfung von Würfel mit Kugel: