6.1 – Punktwolken

Eine Punktwolke (englisch point cloud) ist eine Menge von Punkten eines Vektorraums, die eine unorganisierte räumliche Struktur („Wolke“) aufweist.^[1] Eine Punktwolke ist durch die enthaltenen Punkte beschrieben, die jeweils durch ihre Raumkoordinaten erfasst sind. Punktwolken mit Georeferenzierung enthalten Punkte in einem erdbezogenen Koordinatensystem. Zu den Punkten können zusätzlich Attribute, wie z. B. geometrische Normalen, Farbwerte, Aufnahmezeitpunkt oder Messgenauigkeit, erfasst sein.

Die Erzeugung kann grundsätzlich über Scanning-Verfahren (z. B. terrestrisches oder flugzeuggestütztes Laserscanning) oder photogrammetrische Verfahren^[2] erfolgen sowie allgemein mittels Abtastung von Objektoberflächen durch Systeme wie Koordinatenmessmaschinen oder tastende 3D-Scanner. Optische Scanner untergliedert man in Lasertechnologie, die nach dem Triangulationsprinzip arbeiten, und Normallicht-Scanner, die nach dem Streifenlichtverfahren („coded-light“) arbeiten. Einen zusammenfassenden Überblick über die Vielfalt und Leistungsfähigkeit aktueller optischer Scanning-Methoden und die Weiterverarbeitung der resultierenden 3D-Daten/Punktwolke gibt beispielsweise C. Teutsch.^[3] Durch die mehrfache Erfassung eines räumlichen Ausschnitts zu unterschiedlichen Zeitpunkten lässt sich ein vierdimensionales (zeitvariantes) diskretes räumliches Modell einer Umgebung aufbauen.^[4] Jeder Punkt der Wolke wird dabei zeitlich und räumlich (XYZ-Koordinaten) lokalisiert und kann in weiterer Folge auch georeferenziert werden. (Quelle)

Es gibt viele Möglichkeiten um aus einer Punktwolke eine geschlossene 3D-Oberfläche zu erstellen (z.B. Shrink Wrap, Ball Pivoting oder Point2CAD). Punktewolken und deren Zurückführung in bearbeitbare CAD-Geometrie gewinnt in der Architektur immer wie mehr an Bedeutung, da dies ein effizientes und genaues Mittel der Bestandesaufnahme von existierenden Gebäuden ist.

Abbildung 6.1 – Animiertes Punktwolkenmodell eines Torus

6.2 – Mesh – Diskrete Flächennetze

Untereinander mit Kanten und Flächen verbundene Punkte bilden in der Computergrafik ein , das die Gestalt eines Polyeders definiert. Dreiecksnetze und Vierecksnetze sind hier am geläufigsten.

In der 3D-Computergrafik und der Volumenmodellierung ist ein Polygonnetz eine Sammlung von Scheitelpunkten, Kanten und Flächen, die die Form eines polyedrischen Objekts definieren. Die Flächen bestehen normalerweise aus Dreiecken (Triangle Mesh), Vierecken (Quads) oder anderen einfachen konvexen Polygonen (n-Gons), da dies das Rendern vereinfacht, können aber auch allgemeiner aus konkaven Polygonen oder sogar Polygonen mit Löchern zusammengesetzt sein.

Die Untersuchung von Polygonnetzen ist ein großes Teilgebiet der 3D-Computergrafik und der geometrischen Modellierung. Für unterschiedliche Anwendungen und Ziele werden unterschiedliche Darstellungen von Polygonnetzen verwendet. Die Vielfalt der an Netzen durchgeführten Operationen kann umfassen: Boolesche Logik (konstruktive Festkörpergeometrie), Glättung, Vereinfachung und viele andere. Es gibt auch Algorithmen für Raytracing, Kollisionserkennung und Starrkörperdynamik mit Polygonnetzen. Wenn die Kanten des Netzes anstelle der Flächen gerendert werden, wird das Modell zu einem Drahtgittermodell.

Volumetrische Netze unterscheiden sich von Polygonnetzen dadurch, dass sie explizit sowohl die Oberfläche als auch das Volumen einer Struktur darstellen, während Polygonnetze nur explizit die Oberfläche darstellen (das Volumen ist implizit). Volumetrische Netze finden z.B. in der finiten Elementanalyse Methode (FEA) Anwendung wo zwecks Ermitteln der Verformung oder der Tragfähigkeit eines Elementes dessen Geometrie in viele kleine Polyeder (oft Tetraeder oder Würfel) unterteilt wird.

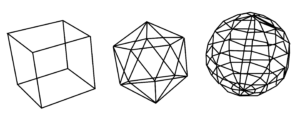
Abbildung 6.2 – Unterschiedliche Drahtgittermodelle, die einfachste Möglichkeit, ein Polygonnetz darzustellen.

Video von Rebecca Allen für Kraftwerk’s „Musique Non Stop“ (1986). Mehr information über das making-of hier.

6.3 – Voxel – Diskrete Volumen

Bei einem räumlichen Datensatz, der in diskretisierter Form in kartesischen Koordinaten vorliegt, bezeichnet Voxel den diskreten Wert an einer XYZ-Koordinate des Datensatzes. (zusammengesetzt aus dem englischen volume vox und el von elements^[1], auch in Anlehnung an das 2D Pendant „Pixel“) bezeichnet in der Computergrafik einen Gitterpunkt („Bild“punkt, Datenelement) in einem dreidimensionalen Gitter. Dies entspricht einem Pixel in einem 2D-Bild, einer Rastergrafik. Wie bei Pixeln wird bei Voxeln üblicherweise die Position nicht explizit gespeichert, sondern implizit aus der Position zu anderen Voxeln hergeleitet. Ein Voxelraum hat eine Auflösung (m,n,o), also Anzahl Zeilen, Spalten und Ebenen. Im Gegensatz dazu werden bei Punkten oder Polygonen die Positionen der Eckkoordinaten gespeichert. (Quelle)

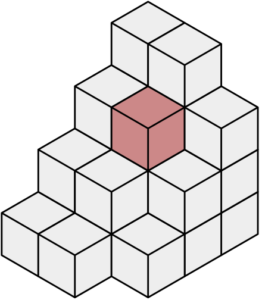
Abbildung 6.3 – Eine Menge von gestapelten Voxeln. Ein einziges ist hervorgehoben.

6.4 – Implizite Flächen

sind Flächen, die im Raum benachbarte Punkte gleicher Merkmale oder Werte einer bestimmten Größe wie zum Beispiel Temperatur oder Dichte miteinander verbinden. Sie sind das dreidimensionale Gegenstück zu Isolinien, die Punkte auf einer Fläche verbinden. Die Bedeutung von Isoflächen liegt in der computergraphischen Visualisierung von Skalarfeldern bzw. Gittern. (Quelle)

Isolinien werden für die wissenschaftliche Visualisierung verwendet. In geografischen Karten wird die Topographie üblicherweise mit Hilfe von Höhenstufen (d. h. Kurven konstanter Höhe über dem Meeresspiegel) visualisiert (Abbildung 12.41). In Wetterkarten wird die Visualisierung oft durch Isolinien wichtiger Messdaten wie Temperatur oder Luftdruck ergänzt.

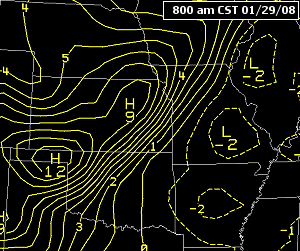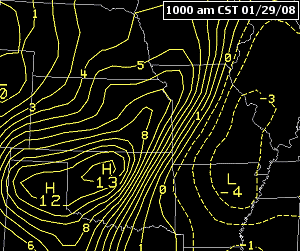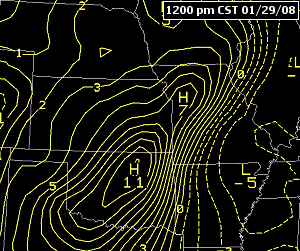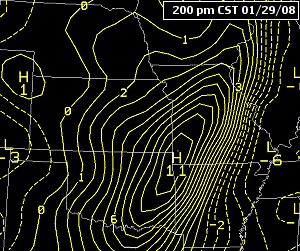
Abbildung 6.5 – Video loop of isallobars showing the motion of a cold front

Es gibt viele Wege, 3d Isoflächen zu rendern, die beiden gebräuchlichsten sind Raycasting und der Marching-Cubes-Algorithmus der die implizite Fläche zuerst in ein Mesh / Polygonnetz übersetzt.

6.4.1 – Signed Distance Functions

oder kurz SDFs geben, wenn sie die Koordinaten eines Punktes im Raum übergeben, den kürzesten Abstand zwischen diesem Punkt und einer Oberfläche zurück. Das Vorzeichen des Rückgabewerts gibt an, ob sich der Punkt innerhalb oder außerhalb dieser Oberfläche befindet (daher vorzeichenbehaftete Abstandsfunktion).

Beispiel

Schauen wir uns ein Beispiel an. Stellen Sie sich eine Kugel vor, die im Ursprung zentriert ist. Die Distanzfunktion der Kugel mit Zentrum C und radius r für Punkt P ist wie folgt:

[latex]f(x,y,z) = \sqrt {\left( {x_C - x_P } \right)^2 + \left( {y_C - y_P } \right)^2 + \left( {z_C - z_P } \right)^2} - r[/latex]

Punkte innerhalb der Kugel haben einen Abstand vom Ursprung, der kleiner als der Radius ist, Punkte auf der Kugel haben einen Abstand, der gleich dem Radius ist, und Punkte außerhalb der Kugel haben einen Abstand, der größer als der Radius ist. Also sieht unsere erste SDF für eine Kugel mit Radius 1 am Ursprung zentriert so aus:

[latex]f(1,0,0)=0 \\ f(0,0,0.5)=−0.5 \\ f(0,3,0)=2[/latex]

Großartig, (1, 0, 0) befindet sich auf der Oberfläche, (0, 0, 0.5) befindet sich innerhalb der Oberfläche, wobei der nächste Punkt auf der Oberfläche 0.5 Einheiten entfernt ist , und (0, 3, 0) liegt außerhalb der Oberfläche, wobei der nächste Punkt auf der Oberfläche 2 Einheiten entfernt ist.

Mehr Informationen zum Modellieren mit SDFs gibt es hier: dbt.arch.ethz.ch/research-stream/volumetric-modelling

6.4.2 – Metaballs

, auch bekannt als „Blobs“ oder „weiche Objekte“, folgen dem gleichen Prinzip. Ihre Form wird durch Eingabeformen gesteuert, bei denen es sich in der Regel um einfache Objekte wie Punkte, Linien und einfache Oberflächen handelt. Unter Verwendung des Abstands zu den Eingabeformen wird jede Eingabeform einer lokalen Feldfunktion zugeordnet. Diese lokalen Feldfunktionen werden summiert, was eine Funktion f(x,y,z) ergibt. Seine Niveaumengen f (x,y,z) = k sind die interessierenden Flächen. Ein Beispiel wird gezeigt.^[1]

Ein Metaball ist das Ergebnis eines Algorithmus, der eine dehnbare Oberfläche erzeugt, die die Form einer Kugel (bei genau einem) oder eine Menge von ineinander gehenden Kugeln erzeugt. Der Algorithmus wurde in den frühen 1980ern von Jim Blinn entwickelt. Ein Metaball ist als eine Funktion in $n$ Dimensionen definiert, für die üblichen drei Dimensionen also entsprechend $f(x,y,z)$ . Um ein Volumen zu erzeugen wird ein Schwellenwert gewählt. (Quelle)

\sum _{i=0}^{n}{\mathit {Metaball}}_{i}(x,y,z)\leq {\mathit {Schwellenwert}}

definiert dann, ob der von $n$ Metaballs definierte Körper am Punkt $(x,y,z)$ gefüllt ist. Eine typische Metaball-Funktion ist

f(x,y,z)={\frac {1}{(x-x_{0})^{2}+(y-y_{0})^{2}+(z-z_{0})^{2}}}

wobei $(x_{0},y_{0},z_{0})$ das Zentrum des Balles angibt und $(x,y,z)$ den zu untersuchenden Punkt. $f(x,y,z)$ gibt dann also die Stärke des Balles an diesem Punkt zurück. Ist die Summe der Stärken aller Bälle an diesem Punkt größer als der Schwellenwert, so ist der Körper dort gefüllt, d.h. der Punkt liegt innerhalb des Blobs. Da die Funktion auf Grund der Division rechenintensiv ist, werden auch polynomiale Annäherungen verwendet.