7.1 – Topologie
Die (griechisch τόπος tópos, deutsch ‚Ort, Platz, Stelle‘ und -logie) ist die Lehre von der Lage und Anordnung geometrischer Gebilde im Raum und ein fundamentales Teilgebiet der Mathematik. Sie beschäftigt sich mit den Eigenschaften mathematischer Strukturen, die unter stetigen Verformungen erhalten bleiben, wobei der Begriff der Stetigkeit durch die Topologie in sehr allgemeiner Form definiert wird. Die Topologie ging aus den Konzepten der Geometrie und Mengenlehre hervor. Die geometrische Topologie ist ein Teilgebiet der Mathematik, das sich mit Mannigfaltigkeiten (engl. Manifold) und deren Einbettungen beschäftigt.

Abbildung 7.1 – Tasse und Volltorus sind zueinander homöomorph. Anmerkung: Ein Homöomorphismus ist eine direkte Abbildung zwischen den Punkten der Tasse und des Volltorus, die Zwischenstufen im zeitlichen Verlauf dienen nur der Illustration der Stetigkeit dieser Abbildung.
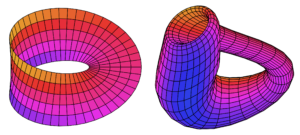
Abbildung 7.2 – Mathematisch gesehen ist das Möbiusband (links) eine nicht-orientierbare Mannigfaltigkeit. Eine weitere Fläche, die in diese Kategorie gehört, ist die Kleinsche Flasche (rechts)
Unter dem Geschlecht einer kompakten orientierbaren Fläche versteht man in der Topologie die Anzahl der „Löcher“ (oder der „Henkel“) der Fläche.

Abbildung 7.3 – Flächen mit Geschlecht 1, 2 und 3.
Die Mannigfaltigkeit einer Topologie erlaubt Rückschlüsse darauf, ob sich das Objekt 3D drucken lässt, denn diese gibt an, ob ein klar definiertes Innen und Aussen existiert.
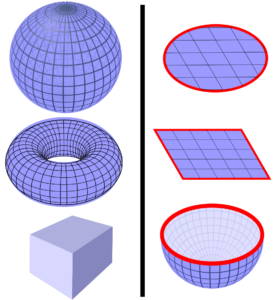
Abbildung 7.4 – Auf der linken Seite sind Mannigfaltigkeiten ohne Rand und auf der rechten Seite sind Mannigfaltigkeiten mit Rand abgebildet. Diese sind nicht direkt 3D druckbar, weil kein Innen und Aussen definiert ist.
7.2 – Graphen
Ein ist in der Graphentheorie eine abstrakte Struktur, die eine Menge von Objekten zusammen mit den zwischen diesen Objekten bestehenden Verbindungen repräsentiert. Die mathematischen Abstraktionen der Objekte werden dabei Knoten des Graphen genannt. Die paarweisen Verbindungen zwischen Knoten heißen Kanten Die Kanten können gerichtet oder ungerichtet sein. Häufig werden Graphen anschaulich gezeichnet, indem die Knoten durch Punkte und die Kanten durch Linien dargestellt werden.[2]
Beispiel
Anschauliche Beispiele für Graphen sind ein Stammbaum oder das U-Bahn-Netz einer Stadt (siehe Abbildungen). Bei einem Stammbaum stellt jeder Knoten ein Familienmitglied dar und jede Kante ist eine Verbindung zwischen einem Elternteil und einem Kind. In einem U-Bahn-Netz stellt jeder Knoten eine U-Bahn-Station dar und jede Kante eine direkte Zugverbindung zwischen zwei Stationen.
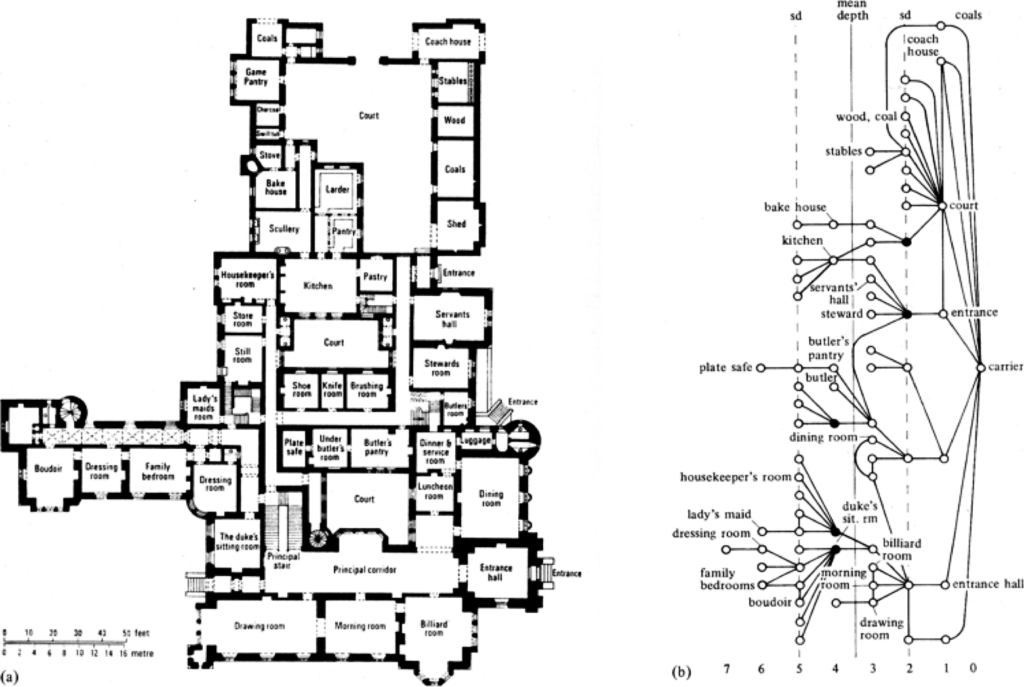
Abbildung 7.5 – Steadman, J. P. 1983. Architectural Morphology an Introduction to the Geometry of Building Plans
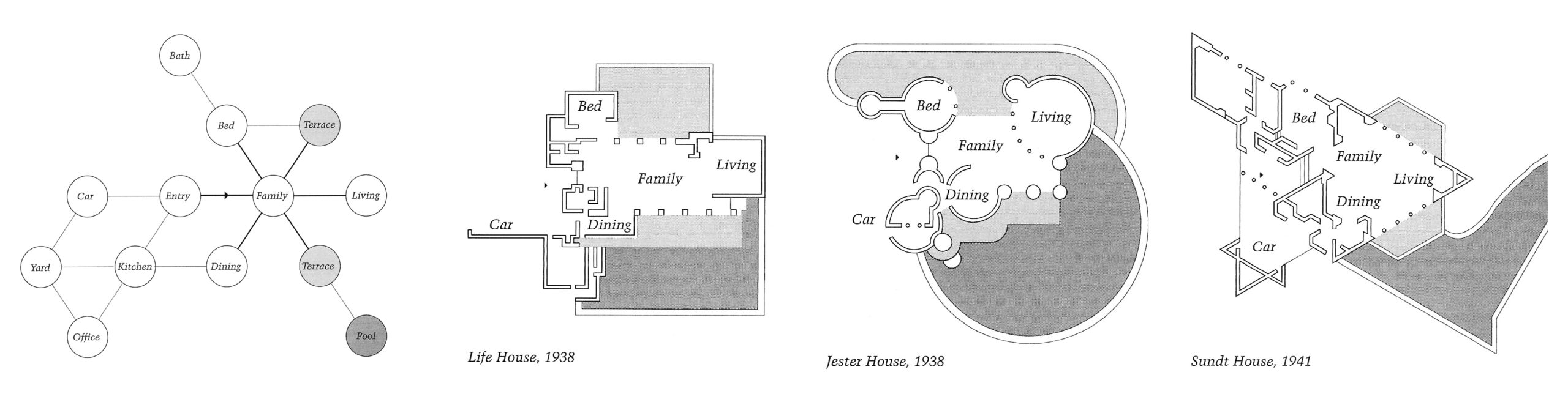
Abbildung 7.6 – Frank Lloyd Wright in Mitchell, William John. 1990. The Logic of Architecture. Mit Press

Abbildung 7.7 – Peter Eisenmann, THE MAX REINHARDT HAUS, Location: Berlin, Germany, Year: 1992

Abbildung 7.8 – Un Studio, Möbius House

Abbildung 7.9 – National Taichung Theater von Toyo Ito & Associates

Abbildung 7.10 – NonLin/Lin von Marc Fornes und The Very Many

Abbildung 7.11 – OMA — Jussieu Library
Die Topologie (griechisch τόπος tópos, deutsch ‚Ort, Platz, Stelle‘ und -logie) ist die Lehre von der Lage und Anordnung geometrischer Gebilde im Raum und ein fundamentales Teilgebiet der Mathematik. Sie beschäftigt sich mit den Eigenschaften mathematischer Strukturen, die unter stetigen Verformungen erhalten bleiben, wobei der Begriff der Stetigkeit durch die Topologie in sehr allgemeiner Form definiert wird.
Ein Graph ist in der Graphentheorie eine abstrakte Struktur, die eine Menge von Objekten zusammen mit den zwischen diesen Objekten bestehenden Verbindungen repräsentiert. Die mathematischen Abstraktionen der Objekte werden dabei Knoten des Graphen genannt. Die paarweisen Verbindungen zwischen Knoten heißen Kanten Die Kanten können gerichtet oder ungerichtet sein. Häufig werden Graphen anschaulich gezeichnet, indem die Knoten durch Punkte und die Kanten durch Linien dargestellt werden.[2]